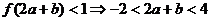1.设复数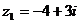 ,
,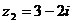 ,则复数
,则复数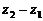 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.某中学高一年级有学生1200人,高二年级有学生900人,高三年级有学生1500人,现用分层抽样的方法从中抽取一个容量为720的样本进行某项调查,则高二年级应抽取的学生数为( )
A.180
B.
3.“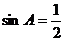 ”是“
”是“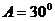 ”的( )条件
”的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
4.在边长为1的等边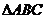 中,设
中,设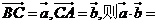 ( )
( )
A.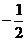 B.
B.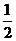 C.
C.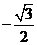 D.
D.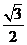
5.下列命题错误的是( )
A.命题“若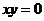 ,则
,则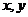 中至少有一个为零”的否定是:“若
中至少有一个为零”的否定是:“若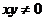 ,则
,则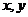 都不为零”。
都不为零”。
B.对于命题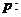
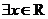 ,使得
,使得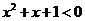 ;则
;则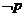 是
是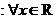 ,均有
,均有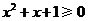 。
。
C.命题“若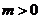 ,则方程
,则方程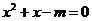 有实根”的逆否命题为:“若方程
有实根”的逆否命题为:“若方程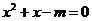 无实根,则
无实根,则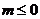 ”。
”。
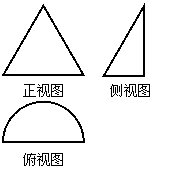 D.“
D.“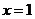 ”是“
”是“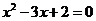 ”的充分不必要条件。
”的充分不必要条件。
6.如图是某几何体的三视图,其中正视图是腰长为2的
等腰三角形,俯视图是半径为1的半圆,则该几何体
的体积是( )
A.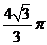 B.
B.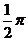 C.
C.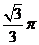 D.
D.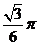
7.直线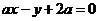 与圆
与圆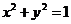 的位置关系是( )
的位置关系是( )
A.相离 B.相交 C.相切 D.不确定
8. 设集合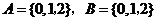 ,分别从集合
,分别从集合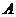 和
和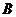 中随机取一个数
中随机取一个数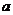 和
和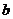 ,确定平面上的一个点
,确定平面上的一个点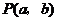 ,记“点
,记“点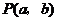 落在直线
落在直线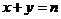 上”为事件
上”为事件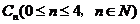 ,若事件
,若事件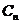 的概率最大,则
的概率最大,则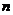 的可能值为( )
的可能值为( )
A.2 B.
9.已知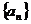 是等差数列,
是等差数列,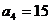 ,
,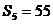 ,则过点
,则过点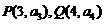 的直线的斜率为( )
的直线的斜率为( )
A.4
B.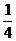 C.-4
D.-14
C.-4
D.-14
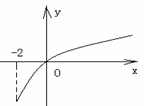 10. 已知函数
10. 已知函数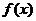 的定义域为[―2,
的定义域为[―2,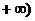 ,部分对应值如下表。
,部分对应值如下表。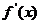 为
为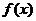 的导函数,函数
的导函数,函数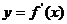 的图象如右图所示:
的图象如右图所示:

―2
0
4
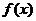
1
―1
1
若两正数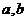 满足
满足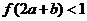 ,则
,则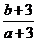 的取值范围是( )
的取值范围是( )
A.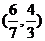 B.
B.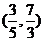 C.
C.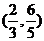 D.
D.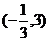
第Ⅱ卷 非选择题(共100分)
11. 函数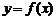 的图像在点M
的图像在点M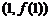 处的切线方程是
处的切线方程是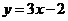 ,
,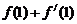 =
。
=
。
12. 已知流程图如右图所示,该程序运行后,为使输出的b值为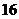 ,则循环体的判断框内①处应填
。
,则循环体的判断框内①处应填
。
13. 以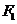 、
、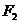 为焦点的椭圆
为焦点的椭圆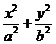 =1(
=1(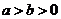 )上顶点P,
)上顶点P,
当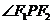 =120°时,则此椭圆离心率e的大小为 。
=120°时,则此椭圆离心率e的大小为 。
★(请考生在以下二个小题中任选一题作答,全答的以第一小题计分)
 14. (坐标系与参数方程选做题)极坐标系中,曲线
14. (坐标系与参数方程选做题)极坐标系中,曲线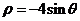 和
和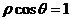 相交于点
相交于点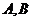 ,则
,则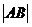 = .
= .
15.(几何证明选讲选做题)如图,圆O是△ABC的外接圆,过点C的
切线交AB的延长线于点D,CD=2,AB =3.
则BD的长为 .
(★请在答题卷的指定区域内作答,否则该题计为零分.)
16.(本小题满分12分)
已知函数 .
.
(Ⅰ)求函数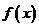 的周期和最大值;
的周期和最大值;
(Ⅱ)已知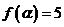 ,求
,求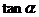 的值.
的值.
17.(本小题满分14分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量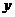 (升)关于行驶速度
(升)关于行驶速度 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: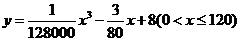 .已知甲、乙两地相距100千米。
.已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
18.(本小题满分12分)
(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒。当你到达路口时,求不是红灯的概率。
(2)已知关于x的一元二次函数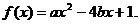 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为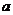 和
和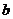 ,求函数
,求函数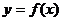 在区间[
在区间[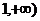 上是增函数的概率。
上是增函数的概率。
19.(本小题满分14分)
如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
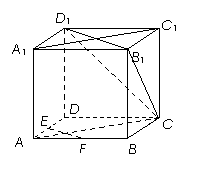 (1)求证:EF∥平面CB1D1;
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
20.(本小题满分14分)
若椭圆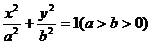 过点
过点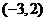 ,离心率为
,离心率为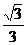 ,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为
,⊙O的圆心在原点,直径为椭圆的短轴,⊙M的方程为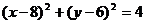 ,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
,过⊙M上任一点P作⊙O的切线PA、PB,切点为A、B.
(1) 求椭圆的方程;
(2)若直线PA与⊙M的另一交点为Q,当弦PQ最大时,求直线PA的方程。
21.(本小题满分14分)
已知数列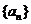 的前
的前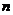 项和
项和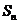 和通项
和通项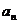 满足
满足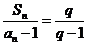 (
(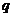 是常数且
是常数且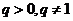 )。
)。
(Ⅰ)求数列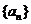 的通项公式;
的通项公式;
(Ⅱ) 当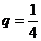 时,试证明
时,试证明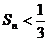 ;
;
(Ⅲ)设函数 ,
,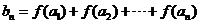 ,是否存在正整数
,是否存在正整数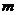 ,使
,使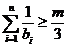 对
对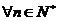 都成立?若存在,求出
都成立?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
惠州市2009届高三模拟考试数学试题
(文科)评分标准
题号
1
2
3
4
5
6
7
8
9
10
答案
D
A
B
A
A
D
D
A
A
B
1、解析: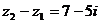 ,所以对应的点的坐标为
,所以对应的点的坐标为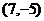 ,故选D。
,故选D。
2、解析:抽取学生数为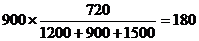 (人),故选A。
(人),故选A。
3、解析: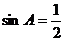
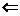
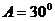 ,故选B。
,故选B。
4、解析: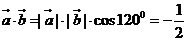 ,故选A。
,故选A。
5、解析:命题的否定是只否定结论,∴选A.
6、解析:由三视图知几何体的直观图是半个圆锥, 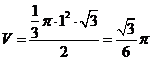 ,∴选D.
,∴选D.
 7、解析:圆心(0,0)到直线的距离
7、解析:圆心(0,0)到直线的距离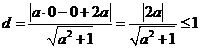 ,
,
圆的半径为1,可能相切或相交。故选D。
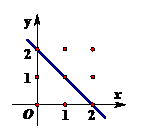
8、解析:P点取法总共有9种,由图知直线截距为2时经过的点最多;
∴选A.
9、解析:∵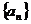 是等差数列,
是等差数列,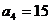 ,
,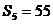 ,
,
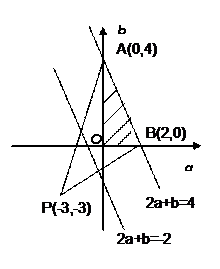 ∴
∴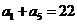 ,
,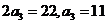 ,∴
,∴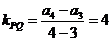 ,选A.
,选A.
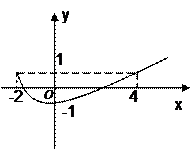 10、解析:由题意,函数
10、解析:由题意,函数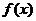 的图象大致如图,
的图象大致如图,
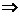
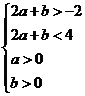 ,
,
则由不等式组所表示的区域如图所示,
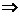
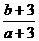 的取值范围即区域内的点与
的取值范围即区域内的点与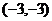
连线的斜率的取值范围,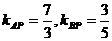 ,故选B。
,故选B。
二.填空题(本大题共5小题,每小题5分,满分20分.其中14~15题是选做题,考生只需选做其中一题,两题全答的,只以第一小题计分.)
11、4 12、3(注:答题卷填的是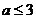 也给5分) 13、
也给5分) 13、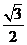 14、
14、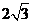 15、4
15、4
11、解析:∵切点既在曲线上也在切线上,∴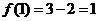 ,
,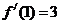 ,∴
,∴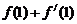 =4
=4
12、解析: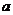 =1时进入循环此时
=1时进入循环此时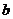 =21=2,
=21=2,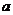 =2时再进入循环此时
=2时再进入循环此时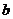 =22=4,
=22=4,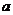 =3时再进入循环此时
=3时再进入循环此时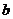 =24=16,∴
=24=16,∴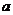 =4时应跳出循环,∴循环满足的条件为
=4时应跳出循环,∴循环满足的条件为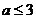 ,∴填3。
,∴填3。
(注:答题卷填的是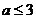 也给5分)
也给5分)
13、解析:当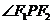 =120°时,
=120°时,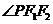 =30°,∴
=30°,∴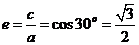 。∴填
。∴填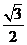 .
.
14、解析:在平面直角坐标系中,曲线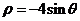 和
和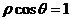 分别表示圆
分别表示圆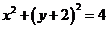 和直线
和直线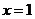 ,作图易知
,作图易知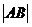 =
=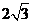 。
。
15、解析:由切割线定理得: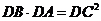 ,
, 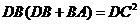 ,
, 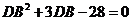 ,
,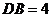 .
.
16.(本小题满分12分)
解:(Ⅰ)
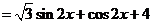
=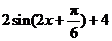 .…………………………………………………… 3分
.…………………………………………………… 3分
∴周期为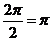 , …………………………………………………… 4分
, …………………………………………………… 4分
最大值为6 …………………………………………………………………… 5分
(Ⅱ)由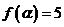 ,得
,得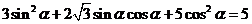 .………………… 6分
.………………… 6分
∴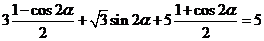 . …………………………… 7分
. …………………………… 7分
∴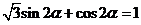 , ………………………………………………… 8分
, ………………………………………………… 8分
即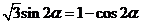
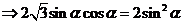 ………… 9分
………… 9分
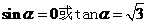 , ………………………………………………………10分
, ………………………………………………………10分
∴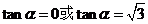 . …………………………………………………… 12分
. …………………………………………………… 12分
17.(本小题满分14分)
解:(I)当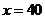 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了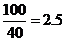 小时, ………………2分
小时, ………………2分
要耗油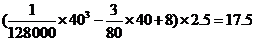 (升)。
……4分
(升)。
……4分
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。……6分
(II)当速度为 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了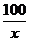 小时,设耗油量为
小时,设耗油量为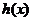 升,
升,
依题意得
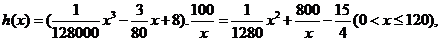 …………8分
…………8分
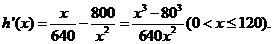 令
令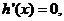 得
得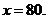 ………10分
………10分
当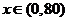 时,
时,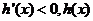 是减函数;
是减函数;
当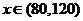 时,
时,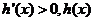 是增函数。
是增函数。
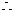 当
当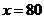 时,
时,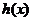 取到极小值
取到极小值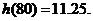 ………………12分
………………12分
因为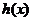 在
在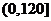 上只有一个极值,所以它是最小值。
上只有一个极值,所以它是最小值。
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少为11.25升。…14分
18.(本小题满分12分)
解:(1)基本事件是遇到红灯、黄灯和绿灯,它们的时间分别为30秒、5秒和40秒,设它们的概率的分别为P1,P2,P3,
所以不是红灯的概率P=1- P1=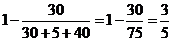 ………………… 6分
………………… 6分
(2)∵函数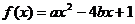 的图象的对称轴为
的图象的对称轴为
要使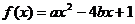 在区间
在区间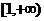 上为增函数,
上为增函数,
当且仅当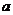 >0且
>0且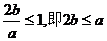 …………………………………………8分
…………………………………………8分
若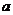 =1则
=1则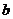 =-1,
=-1,
若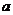 =2则
=2则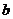 =-1,1;
=-1,1;
若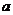 =3则
=3则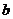 =-1,1;
…………………………………………10分
=-1,1;
…………………………………………10分
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为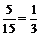 …………………………………………12分
…………………………………………12分
19.(本小题满分14分)
(1)证明:连结BD.在长方体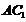 中,对角线
中,对角线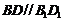 .
……………2分
.
……………2分
又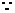 E、F为棱AD、AB的中点, ∴
E、F为棱AD、AB的中点, ∴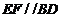 . ∴
. ∴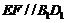 . ……………4分
. ……………4分
又B1D1平面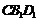 ,
,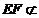 平面
平面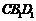 ,∴EF∥平面CB1D1.
……………7分
,∴EF∥平面CB1D1.
……………7分
(2)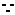 在长方体
在长方体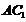 中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
中,AA1⊥平面A1B1C1D1,而B1D1平面A1B1C1D1,
∴AA1⊥B1D1. ………………………9分
又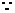 在正方形A1B1C1D1中,A1C1⊥B1D1,∴ B1D1⊥平面CAA1C1.
在正方形A1B1C1D1中,A1C1⊥B1D1,∴ B1D1⊥平面CAA1C1.
又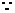 B1D1平面CB1D1,∴平面CAA1C1⊥平面CB1D1.
……………14分
B1D1平面CB1D1,∴平面CAA1C1⊥平面CB1D1.
……………14分
20.(本小题满分14分)
解:(1)由题意得: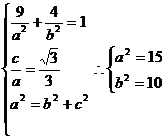 ,
………………………4分
,
………………………4分
所以椭圆的方程为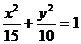 …………………………………………6分
…………………………………………6分
(2)由题可知当直线PA过圆M的圆心(8,6)时,弦PQ最大, ……8分
因为直线PA的斜率一定存在,设直线PA的方程为:y-6=k(x-8) ……10分
又因为PA与圆O相切,所以圆心(0,0)到直线PA的距离为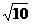 ……11分
……11分
即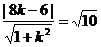 可得
可得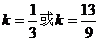 ……………………12分
……………………12分
所以直线PA的方程为: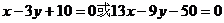 …………14分
…………14分
21.(本小题满分14分)
解: (Ⅰ)由题意,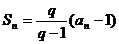 ,得
,得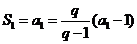
 ∴
∴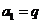 …………1分
…………1分
当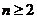 时,
时, 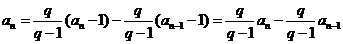 ,
,
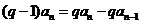 ∴
∴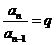 ………………3分
………………3分
∴数列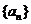 是首项
是首项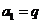 ,公比为
,公比为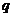 的等比数列,∴
的等比数列,∴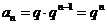 ………4分
………4分
(Ⅱ)由(Ⅰ)知当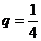 时,
时,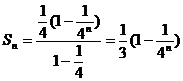 …………………5分
…………………5分
∵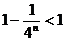 ,∴
,∴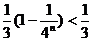 …………………………………………………6分
…………………………………………………6分
即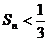 …………………………………………………………………………7分
…………………………………………………………………………7分
(Ⅲ)∵

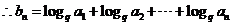 =
=
=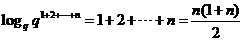 ………………………………9分
………………………………9分
∵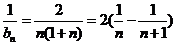 ………………………………………………10分
………………………………………………10分
∴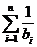
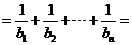
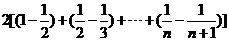 =
=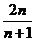 …12分
…12分
由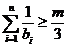 得
得
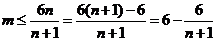 -------(
-------(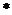 )
)
∵(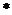 )对
)对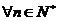 都成立 ∴
都成立 ∴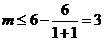 ∵
∵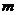 是正整数,∴
是正整数,∴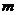 的值为1,2,3。
的值为1,2,3。
∴使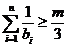 对
对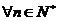 都成立的正整数
都成立的正整数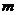 存在,其值为:1,2,3. ……14分
存在,其值为:1,2,3. ……14分