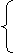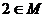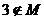1.已知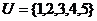 ,
,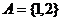 ,
,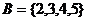 ,则
,则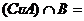
A.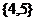 B.
B.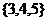 C.
C.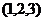 D.
D.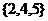
2.已知数列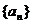 为等差数列,且
为等差数列,且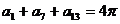 ,则
,则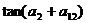
A.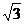 B.
B.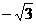 C.
C.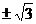 D.
D.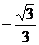
3.设函数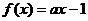 ,且
,且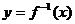 的图象过点
的图象过点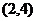 ,则
,则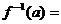
A.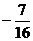 B.
B.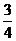 C.
C.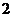 D.
D.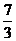
4.将函数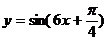 的图象上各点的横坐标伸长到原来的
的图象上各点的横坐标伸长到原来的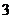 倍,再向右平移
倍,再向右平移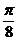 个单位,得到的函数的一个对称中心是
个单位,得到的函数的一个对称中心是
A.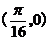 B.
B.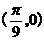 C.
C.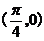 D.
D.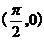
5.复数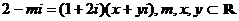 ,且
,且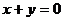 ,则
,则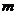 的值
的值
A.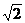 B.
B.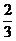 C.-
C.-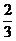 D.
D.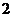
6.设二项式 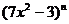 的展开式中各项系数之和为
的展开式中各项系数之和为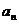 ,二项式
,二项式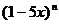 的展开式中各项的二项式系数之和为
的展开式中各项的二项式系数之和为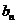 ,且点
,且点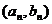 在直线
在直线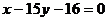 上,则
上,则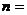
A.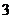 B.
B.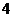 C.
C.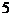 D.
D.
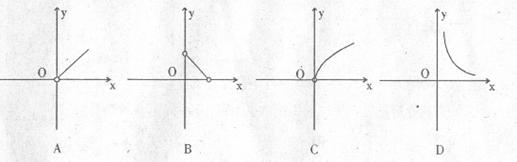
7 一个棱锥被平行于底面的截面截成一个小棱锥(记为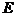 )和另一个几何体(记为
)和另一个几何体(记为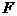 ),若
),若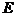 的体积为
的体积为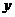 ,
,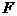 的体积为
的体积为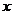 ,则
,则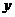 关于
关于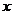 的函数图象大致形状为
的函数图象大致形状为
8.若方程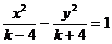 表示双曲线,则它的焦点坐标为
表示双曲线,则它的焦点坐标为
A.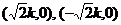 B.
B.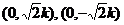
C.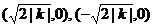 D.由
D.由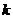 决定
决定
9已知直线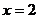 及
及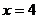 与函数
与函数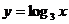 的图象的交点分别为
的图象的交点分别为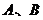 ,与函数
,与函数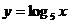 的图象的交点分别为
的图象的交点分别为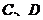 ,则直线
,则直线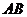 与
与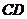
A.平行 B.相交且交点在第二象限
C.相交且交点在第三象限 D.相交且交点是原点
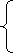
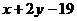 ≥
≥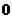
10.设二元一次不等式组所 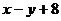 ≥
≥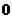 表示的平面区域为
表示的平面区域为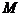 ,使函数
,使函数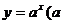
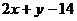 ≤
≤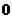
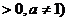 的图象过区域
的图象过区域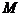 的
的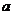 的取值范围是
的取值范围是
A.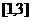 B.
B.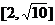 C.
C.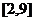 D.
D.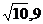
11.连续掷骰子两次得到的点数分别为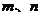 ,作向量
,作向量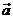
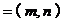 ,则与向量
,则与向量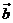
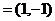 的夹角成为直角三角形内角的概率是
的夹角成为直角三角形内角的概率是
A.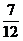 B.
B.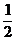 C.
C.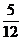 D.
D.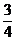
12.已知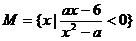 ,且
则
,且
则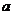 的取值范围是
的取值范围是
A.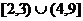 B.
B.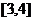 C.
C.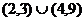 D.
D.
吉安市高三第一次模拟考试
理 科 数 学
第Ⅱ卷
注意事项:
第Ⅱ卷2页,须用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
13.某工厂生产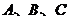 三种不同型号的产品,产品数量之比为
三种不同型号的产品,产品数量之比为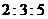 ,现用分层抽样的方法抽出一个容量为
,现用分层抽样的方法抽出一个容量为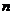 的样本,样本中
的样本,样本中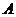 型产品有
型产品有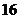 件,则此样本的容量
件,则此样本的容量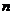 =_________________。
=_________________。
14.已知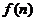 满足
满足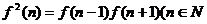 且
且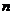 ≥2
≥2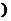 ,若
,若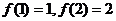 则
则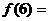 _______________。
_______________。
15.在体积为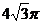 的球的表面上有
的球的表面上有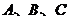 三点,
三点,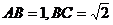 。
。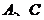 两
两
点的球面距离为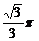 ,则
,则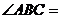 ______________。
______________。
16.给出下列命题:
①不存在实数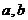 使
使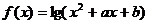 的定义域、值域均为一切实数;
的定义域、值域均为一切实数;
②函数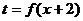 图象与函数
图象与函数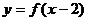 图象关于直线
图象关于直线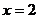 对称;
对称;
③函数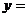
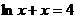 有且只有一个实数根;
有且只有一个实数根;
④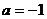 是方程
是方程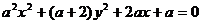 表示圆的充分必要条件。
表示圆的充分必要条件。
其中真命题的序号是______________________。(写出所有真命题的序号)
17.(本小题满分12分)
已知向量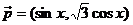 ,
,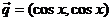 ,定义函数
,定义函数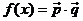
(1)求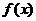 的最小正周期
的最小正周期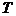 ;
;
(2)若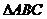 的三边长
的三边长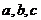 成等比数列,且
成等比数列,且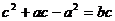 ,求边
,求边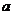 所对角
所对角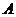 以及
以及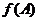 的大小。
的大小。
18.(本小题满分12分)
等差数列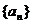 的公差不为零,
的公差不为零,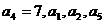 成等比数列,数列
成等比数列,数列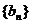 满足:
满足:
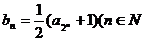 ※
※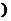
(1) 求数列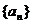 、
、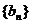 的通项公式;
的通项公式;
(2) 求数列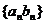 的前
的前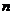 项和
项和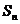 。
。
19.(本小题满分12分)
一个盒子装有完全相同的6张卡片,上面分别写着如下6个定义域均为R的函数:
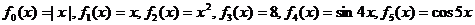 。
。
(1)从盒子中随机取出2张卡片,将卡片上的两个函数相加得一个新的函数,求所得函数是偶函数的概率;
 (2)从盒子中不放回地取卡片,每次取出一张,直至写有奇函数的卡片被全部取出为止,求抽取次数恰为3的概率。
(2)从盒子中不放回地取卡片,每次取出一张,直至写有奇函数的卡片被全部取出为止,求抽取次数恰为3的概率。
20.(本小题满分12分)
如图,在直四棱柱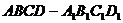 中,
中,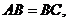
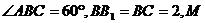 为
为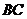 中点,点
中点,点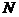 在
在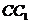 上。
上。
(1)试确定点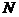 的位置,使
的位置,使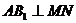 ;
;
(2)当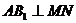 时,求二面角
时,求二面角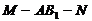 的正切值。
的正切值。
21.(本小题满分12分)
已知函数 ≥
≥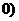
(1) 若函数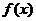 的极小值为
的极小值为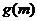 ,求集合
,求集合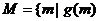 ≥
≥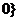 ;
;
(2) 对于(1)中集合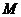 ,任取
,任取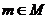 ,函数
,函数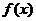 在区间
在区间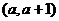 都是增函数,求
都是增函数,求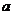 的取值范围。
的取值范围。
22.(本小题满分14分)
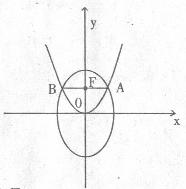
已知椭圆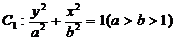 与抛物线
与抛物线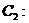
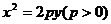 的交点分别为
的交点分别为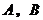 ,如图所示,
,如图所示,
(1)若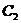 的焦点恰好是
的焦点恰好是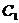 的上焦点
的上焦点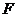 ,且;
,且;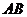 过点
过点
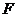 ,求
,求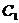 的离心率;
的离心率;
(2)设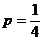 且抛物线
且抛物线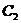 在
在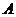 点处的切线
点处的切线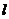 与
与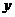 轴的交点为
轴的交点为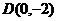 ,求
,求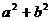 的最小值和此时椭圆的方程。
的最小值和此时椭圆的方程。
吉安市高三第一次模拟考试理科数学试卷