1.已知集合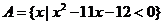 ,集合
,集合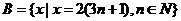 ,则
,则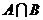 =
=
2.若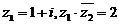 ,则
,则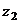 =
=
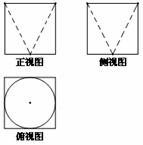
3.一个容器的外形是一个棱长为2的正方体,其三视图
如图所示,则容器的容积为
4.已知点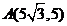 ,过点
,过点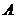 的直线
的直线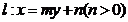 ,若可行域
,若可行域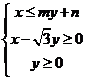
的外接圆的直径为20,则实数
5.若向量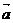 =
=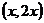 ,
,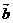 =
=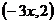 ,且
,且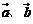 的夹角为钝角,则
的夹角为钝角,则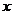 的取值范围是____________
的取值范围是____________
6.已知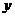
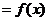 是偶函数,当
是偶函数,当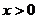 时
时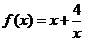 ,且当
,且当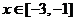 时
时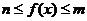 恒成立.则
恒成立.则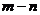 的值是
的值是
7.等差数列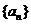 中.
中.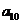 < 0 ,
< 0 ,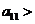 0 .且
0 .且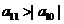 ,
,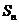 为数列
为数列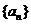 的前
的前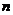 项和,则使
项和,则使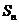 > 0 的
> 0 的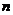 的最小值为
的最小值为
8.若将函数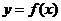 的图象按向量
的图象按向量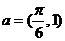 平移后得到函数
平移后得到函数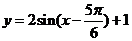 的图象,则函数
的图象,则函数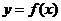 单调递增区间是
单调递增区间是
9.在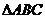 中,已知角
中,已知角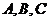 所对的边分别是
所对的边分别是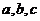 ,且
,且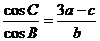 ,又
,又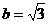 ,则
,则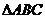 的面积的最大值为
的面积的最大值为
10.下列程序运行结果为
i←1
While i<7
i←i+2
s←2i+3
End While
Print s
End
11. 已知区域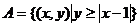 ,区域
,区域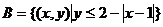 ,点
,点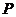 在区域
在区域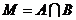 ,则
,则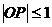 的概率是
的概率是
12.已知椭圆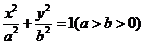 与双曲线
与双曲线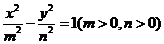 有相同的焦点
有相同的焦点 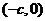 (c,0)若c是
(c,0)若c是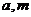 的等比中项,
的等比中项,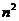 是
是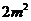 与
与 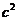 的等差中项,则椭圆的离心率
的等差中项,则椭圆的离心率
是
 13.对于在区间[a,b]上有意义的两个函数
13.对于在区间[a,b]上有意义的两个函数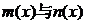 ,如果对于区间[a,b]中的任意x均有
,如果对于区间[a,b]中的任意x均有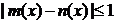 ,则称
,则称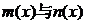 在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数
在[a,b]上是“密切函数”, [a,b]称为“密切区间”,若函数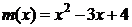 与
与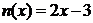 在区间[a,b]上是“密切函数”,则密切区间为
在区间[a,b]上是“密切函数”,则密切区间为
14. 给定正整数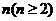 按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,
按右图方式构成倒立三角形数表,第一行依次写上数l,2,3,…,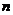 ,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依次类推,最后一行(第
,在第一行的每相邻两个数正中间的下方写上这两个数之和,得到第二行的数(比上一行少一个数),依次类推,最后一行(第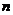 行)只有一个数,例如
行)只有一个数,例如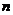 =6时数表如图所,则当
=6时数表如图所,则当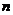 =2009时最后一行的数是
.
=2009时最后一行的数是
.
 15. (本小题共14分)
15. (本小题共14分)
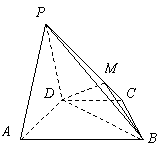
如图,在四棱锥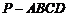 中,平面
中,平面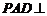 平面
平面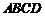 ,
,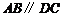 ,
,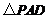 是等边三角形,已知
是等边三角形,已知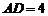 ,
,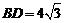 ,
,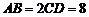 .
.
(Ⅰ)设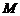 是
是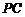 上的一点,证明:平面
上的一点,证明:平面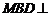 平面
平面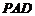 ;
;
(Ⅱ)当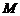 点位于线段PC什么位置时,
点位于线段PC什么位置时,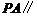 平面
平面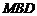 ?
?
(Ⅲ)求四棱锥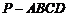 的体积.
的体积.
16.(本小题共14分)
已知二次函数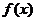 对任意
对任意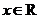 ,都有
,都有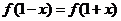 成立,设向量
成立,设向量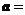 (sinx,2),
(sinx,2),
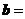 (2sinx,
(2sinx,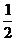 ) ,
) ,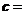 (cos2x,1) ,
(cos2x,1) ,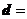 (1,2), 当
(1,2), 当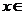 [0,
[0,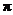 ]时,
]时,
求不等式f(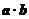 )>f(
)>f(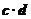 )的解集.
)的解集.
17.(本小题共15分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量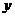 (升)关于行驶速度
(升)关于行驶速度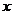 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: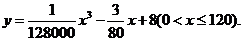 已知甲、乙两地相距
已知甲、乙两地相距
(1)当汽车以
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
18. (本小题共15分)
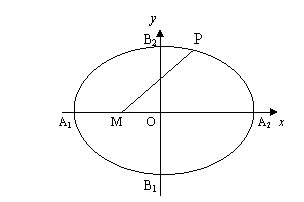
如图,椭圆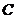 :
: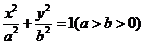 ,
,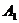 、
、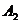 、
、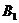 、
、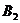 为椭圆
为椭圆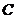 的顶点.
的顶点.
(Ⅰ)设点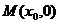 ,若当且仅当椭圆
,若当且仅当椭圆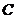 上的点
上的点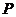 在椭圆的顶点时,
在椭圆的顶点时, 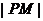 取得最大值与最小值,求
取得最大值与最小值,求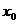 的取值范围;
的取值范围;
(Ⅱ)若椭圆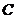 上的点
上的点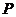 到焦点距离的最大值为
到焦点距离的最大值为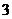 ,最小值为
,最小值为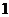 ,且与直线
,且与直线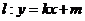 相交于
相交于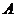 ,
,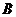 两点(
两点(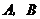 不是椭圆的左右顶点),并满足
不是椭圆的左右顶点),并满足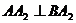 .试研究:直线
.试研究:直线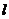 是否过定点?若过定点,请求出定点坐标,若不过定点,请说明理由.
是否过定点?若过定点,请求出定点坐标,若不过定点,请说明理由.
19.(本小题共16分)
已知二次函数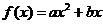 满足条件:①
满足条件:①
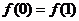 ; ②
; ② 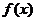 的最小值为
的最小值为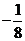 .
.
(1) 求函数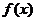 的解析式;
的解析式;
(2) 设数列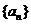 的前
的前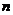 项积为
项积为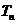 , 且
, 且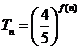 , 求数列
, 求数列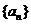 的通项公式;
的通项公式;
(3) 在(2)的条件下, 若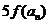 是
是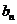 与
与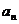 的等差中项, 试问数列
的等差中项, 试问数列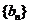 中第几项的值最小? 求出这个最小值.
中第几项的值最小? 求出这个最小值.
20.(本小题共16分)
设函数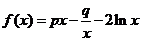 ,且
,且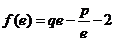 ,其中
,其中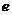 是自然对数的底数.
是自然对数的底数.
(1)求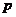 与
与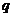 的关系;
的关系;
(2)若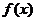 在其定义域内为单调函数,求
在其定义域内为单调函数,求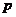 的取值范围;
的取值范围;
(3)设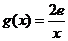 ,若在
,若在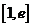 上至少存在一点
上至少存在一点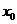 ,使得
,使得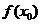 >
>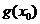 成立,求实数
成立,求实数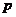 的取值范围.
的取值范围.
江苏省2009届高三南京市高考预测卷