1. 设集合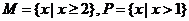 ,那么“
,那么“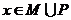 ”是“
”是“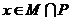 ”的( )
”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2. 若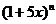 的展开式中各项系数之和为
的展开式中各项系数之和为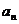 ,
,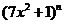 的展开式各项的二项式系数之和为
的展开式各项的二项式系数之和为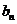 ,则
,则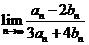 的值是( )
的值是( )
A. 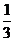 B.
B. 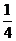 C. 1 D. -
C. 1 D. -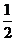
3. 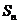 为等差数列
为等差数列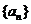 的前n项和,
的前n项和,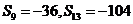 ,等比数列
,等比数列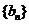 中,
中,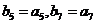 ,则
,则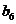 等于( )
等于( )
A. 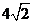 B.
B. 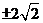 C.
C. 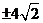 D. 32
D. 32
4. 给出下列四个命题:
1若直线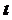 ⊥平面
⊥平面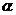 ,
,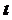 ∥平面
∥平面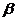 ,则
,则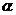 ⊥
⊥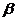 ;
;
2各侧面都是正方形的棱柱一定是正棱柱;
3一个二面角的两个半平面所在平面分别垂直于另一个二面角的两个半平面所在平面,则这两个二面角的平面角互为补角;
4过空间任意一点一定可以作一个和两条异面直线都平行的平面。
其中正确的命题的个数有( )
A. 1 B.
5. 某一批袋装大米,质量服从正态分布N(10,0.01)(单位:kg),任选一袋大米,它的质量是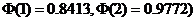
A.
0.8413 B.
6. 已知△ABC的三个顶点在同一球面上,∠BAC=900,AB=AC=2,若球心O到平面ABC的距离为1,则该球的表面积为( )
A. 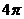 B.
B. 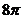 C.
C. 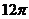 D.
D. 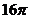
7. 已知正数x、y满足等式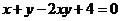 ,则( )
,则( )
A. xy的最大值是2,且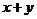 的最小值为4
的最小值为4
B. xy的最小值是4,且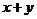 的最大值为4
的最大值为4
C. xy的最大值是2,且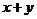 的最大值为4
的最大值为4
D. xy的最小值是4,且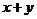 的最小值为4
的最小值为4
8. 在航天员进行的一项太空实验中,先后要实施6个程序,其中程序A只能出现在第一步或最后一步,程序B和C实施时必须相邻,请问实验顺序的编排方法共有( )
A. 24种 B. 48种 C. 96种 D. 144种
9. 已知A、B、C是锐角△ABC的三个内角,向量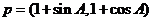 ,
,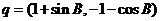 ,则p与q的夹角是( )
,则p与q的夹角是( )
A. 锐角 B. 钝角 C. 直角 D. 不确定
10. 已知函数 在点(1,0)处切线经过椭圆
在点(1,0)处切线经过椭圆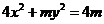 的右焦点,则椭圆两准线间的距离为( )
的右焦点,则椭圆两准线间的距离为( )
A. 6 B.
11. 已知点F1、F2分别是双曲线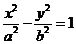 的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若A、B和双曲线的一个顶点构成的三角形为锐角三角形,则该双曲线的离心率e的取值范围是( )
的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A、B两点,若A、B和双曲线的一个顶点构成的三角形为锐角三角形,则该双曲线的离心率e的取值范围是( )
A. 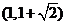 B.
B. 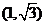 C.
C. 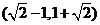 D. (1,2)
D. (1,2)
12. 已知函数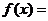 ,若方程
,若方程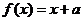 有且只有两个不相等的
有且只有两个不相等的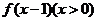
实数根,则实数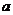 的取值范围是( )
的取值范围是( )
A. 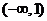 B. (0,1) C.
B. (0,1) C. 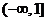 D.
D. 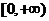
第Ⅱ卷(非选择题,共90分)
13. 已知复数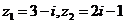 ,
,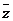 是z的共轭复数,则复数
是z的共轭复数,则复数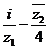 的虚部等于 .
的虚部等于 .
14. 已知x,y满足条件
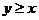 ,则
,则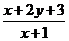 的取值范围是
.
的取值范围是
.
15. 如图是一几何体的平面展开图,其中ABCD为正方形,E、F分别为PA、PD的中点,在此几何体中,给出下面四个结论:
1直线BE与直线CF异面;
2直线BE与直线AF异面;
3直线EF∥平面PBC;
4平面BCE⊥平面PAD.
其中正确的有 个.
16. 在三角形ABC中,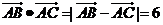 ,M为BC边的中点,则中线AM的长为
. △ABC的面积的最大值为
.
,M为BC边的中点,则中线AM的长为
. △ABC的面积的最大值为
.
17. (本题满分10分)已知函数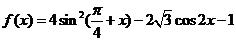 ,且给定条件
,且给定条件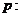 “
“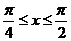 ”.
”.
(1)求 的最大值及最小值;
的最大值及最小值;
(2)若又给条件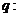 “
“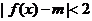 ”且p是q的充分条件,求实数m的取值范围.
”且p是q的充分条件,求实数m的取值范围.
18. (本题满分12分)下面玩掷骰子放球游戏,若掷出1点或6点,甲盒放一球;若掷出2点,3点,4点或5点,乙盒放一球,设掷n次后,甲、乙盒内的球数分别为x、y.
 (1)当n=3时,求x=3,y=0的概率;
(1)当n=3时,求x=3,y=0的概率;
(2)当n=4时,设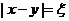 ,求
,求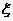 的分布列及数学期望E
的分布列及数学期望E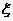 .
.
19. (本题满分12分)如图,在直三棱柱ABC-A1B
AC⊥BC,AC=BC=CC1,D为AB的中点.
(1)求证:AC1∥平面CDB1;
(2)求二面角B-B
20. (本题满分12分)某种商品的成本为5元/ 件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:销售价每上涨1元每天销售量就减少10件;而降价后,日销售量Q(件)与实际销售价x(元)满足关系:
|

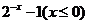

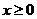
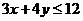
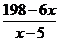
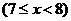
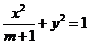 的两个焦点是
的两个焦点是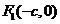 与
与
 ,且椭圆上存在点M,使
,且椭圆上存在点M,使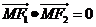 . (1)求实数m 的取值范围;
. (1)求实数m 的取值范围;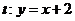 与椭圆存在一个公共点E,使得
与椭圆存在一个公共点E,使得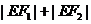 取得最小值,求此最小值及此时椭圆的方程;
取得最小值,求此最小值及此时椭圆的方程;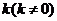 的直线
的直线 ,与椭圆交于不同的两点A、B,满足
,与椭圆交于不同的两点A、B,满足 ,且使得过点Q,N(0,-1)两点的直线NQ满足
,且使得过点Q,N(0,-1)两点的直线NQ满足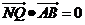 ?若存在,求出k的取值范围;若不存在,说明理由.
?若存在,求出k的取值范围;若不存在,说明理由.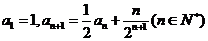 .
.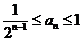 ;
;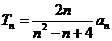 ,且
,且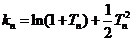 ,证明:
,证明: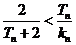 .
.