1.设a + bi= (a,b∈R),则P(a,b)在( )
(a,b∈R),则P(a,b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在某项测量中,测量结果 ~N(2,
~N(2, )(
)( >0),若
>0),若 在(0,2)内取值的概率为0.4,则
在(0,2)内取值的概率为0.4,则 在(0,4)内的概率为(
)
在(0,4)内的概率为(
)
A.0.8 B.
3.已知函数在R上可导,且 = ( )
= ( )
A. B.
B. C.-3 D.3
C.-3 D.3
4.等差数列{an}中,Sn是其前n项和, ,则
,则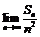 的值为( )
的值为( )
A.2 B.1 C. D.3
D.3
5.能够使圆 恰有两个点到直线
恰有两个点到直线 距离等于1的c的
距离等于1的c的
一个值为 ( )
A. B.
B. C.2 D.3
C.2 D.3
 6.函数y = f (x)是圆心在原点的单位圆的两段圆弧(如图),则不等式f(x)>f (?x) +
x的解集为( )
6.函数y = f (x)是圆心在原点的单位圆的两段圆弧(如图),则不等式f(x)>f (?x) +
x的解集为( )
A.{x| 或
或 }
}
B.{x| 或
或 }
}
C.{x| 或
或 }
}
D.{x| 且x≠0}
且x≠0}
7.在直角坐标平面上, =(1,4),
=(1,4), =(?3,1)且
=(?3,1)且 与
与 在直线l上的射影长度相等,直线l的倾斜角为锐角,则l的斜率为( )
在直线l上的射影长度相等,直线l的倾斜角为锐角,则l的斜率为( )
A. B.
B. C.
C. D.
D.
8.f(x)是偶函数,且f(x)在[0,+∞)上是增函数;不等式f
(ax + 1)≤f (x ?2)对x∈[ ,1]恒成立,则实数a的取值范围是( )
,1]恒成立,则实数a的取值范围是( )
A.[?2,0] B.[?5,0] C.[?5,1] D.[?2,1]
9. 展开式中x3的系数为
.
展开式中x3的系数为
.
10.为配制某种染色剂,需要加入三种有机染料,两种无机染料和两种添加剂,其中有机染料的添加顺序不能相邻,现要研究所有不同添加顺序对染色效果的影响,总共要进行的试验次数为 (用数字作答)
11.当x、y满足约束条件 (k为常数)时,能使z
= x + 3y的最大值为12的k值为
.
(k为常数)时,能使z
= x + 3y的最大值为12的k值为
.
12.已知抛物线y2 = 16x,椭圆 ,则两曲线有公共点时a的最小值为
.
,则两曲线有公共点时a的最小值为
.
 13.如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕边DE旋转过程中的一个图形,现给出下列四个命题:
13.如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′ED是△AED绕边DE旋转过程中的一个图形,现给出下列四个命题:
①动点A′在平面ABC上的射影在线段AF上;
②恒有平面A′GF⊥平面BCED;
③三棱锥A′―FED的体积有最大值;
④异面直线A′E与BD不可能垂直.
其中正确命题的序号是 .
14.对于实数x,符号[x]表示不超过x的最大整数,例如[ ]= 3,[?1.08] = ?2,定义函数f(x) = x ?[x].
]= 3,[?1.08] = ?2,定义函数f(x) = x ?[x].
(i)f(x) 的值域是 ;
(ii) 的最小正周期为 .
的最小正周期为 .
15.如图所示,一个粒子在第一象限及坐标轴上运动,在第一秒内它从原点运动到点(0,1),然后它接着按图所示在x轴、y轴的平行方向来回运动(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…)且每秒移动一个单位长度.(i)粒子运动到(4,4)点时经过了 秒;(ii)第2009秒时,粒子所处的位置为 .
16.某人随机地将编号为1,2,3,4的四个大小相同的小球放入编号为1,2,3,4的四个型号相同的盒子中,每个盒子放一个球,当球的编号与盒子的编号相同时叫做“放法恰当”,否则叫做“放法不恰当”.设放法恰当的情况数为随即变量 .
.
(Ⅰ)求 的分布列;
的分布列;
(Ⅱ)求 的期望与方差.
的期望与方差.
17.已知向量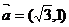 ,向量
,向量 ,
,
(Ⅰ)若 ,且
,且 ,求实数
,求实数 的最小值及相应的
的最小值及相应的 值;
值;
(Ⅱ)若 ,且
,且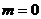 , 求
, 求 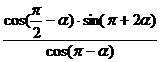 的值.
的值.
18.如图,在边长为12的正方形A1 AA′A1′中,点B、C在线段AA′上,且AB = 3,BC = 4,作BB1∥AA1,分别交A1A1′、AA1′于点B1、P;作CC1∥AA1,分别交A1A1′、AA1′于点C1、Q;将该正方形沿BB1、CC1折叠,使得A′A1′ 与AA1重合,构成如图所示的三棱柱ABC―A1B1C1,在三棱柱ABC―A1B1C1中,
(Ⅰ)求证:AB⊥平面BCC1B1;
(Ⅱ)求面PQA与面ABC所成的锐二面角的大小.
 (Ⅲ)求面APQ将三棱柱ABC―A1B1C1分成上、下两部分几何体的体积之比.
(Ⅲ)求面APQ将三棱柱ABC―A1B1C1分成上、下两部分几何体的体积之比.
19.据中新网2009年4月9日电,日本鹿儿岛县樱岛昭和火山口当地时间9日下午3点31分发生中等规模爆发性喷火,鹿儿岛市及周边飞扬了大量火山灰.火山喷发停止后,为测量的需要距离喷口中心50米内的圆环面为第1区、50米至100米的圆环面为第2区、100米至150米的圆环面为第3区、……、第50(n-1)米至50n米的圆环面为第n区,……,现测得第1区火山灰平均每平方米为1吨、第2区每平方米的平均重量较第1区减少2%、第3区较第2区又减少2%,……,以此类推.
(Ⅰ)若第n区每平方米的重量为an千克,请写出an的表达式;
(Ⅱ)第几区内的火山灰总重量最大?
(Ⅲ)该火山这次喷发出的火山灰的总重量为多少万吨(p 取3,结果精确到万吨)?
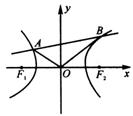 20.如图所示,F1、F2是双曲线x2 ? y2 = 1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y = kx
+ b与圆O相切,并与双曲线交于A、B两点.
20.如图所示,F1、F2是双曲线x2 ? y2 = 1的两个焦点,O为坐标原点,圆O是以F1F2为直径的圆,直线l:y = kx
+ b与圆O相切,并与双曲线交于A、B两点.
(Ⅰ)根据条件求出b和k的关系式;
(Ⅱ)当 ,且满足2≤m≤4时,求△AOB面积的取值范围.
,且满足2≤m≤4时,求△AOB面积的取值范围.
21.设函数f (x) = (b,c∈N*),若方程f(x) = x的解为0,2,且f (?2)<?
(b,c∈N*),若方程f(x) = x的解为0,2,且f (?2)<? .
.
(Ⅰ)试求函数f(x)的单调区间;
(Ⅱ)已知各项不为零的数列{an}满足4Sn・f ( ) = 1,其中Sn为{an}的前n项和.
) = 1,其中Sn为{an}的前n项和.
求证: .
.




