1.集合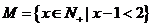 的另一种表示方法是
(
)
的另一种表示方法是
(
)
A.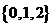 B.
B.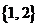 C.
C.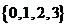 D.
D.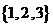
2.若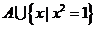
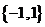 ,则集合
,则集合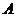 的个数是
( )
的个数是
( )
A.1
B.
 3.如图所示,阴影部分表示的集合是 ( )
3.如图所示,阴影部分表示的集合是 ( )
A.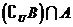 B.
B.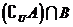
C.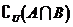 D.
D.
4.与函数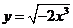 为同一函数的是 ( )
为同一函数的是 ( )
A.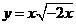 B.
B.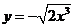
C.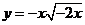 D.
D.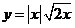
5.函数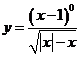 的定义域是
( )
的定义域是
( )
A.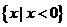 B.
B.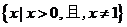
C.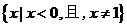 D.
D.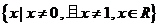
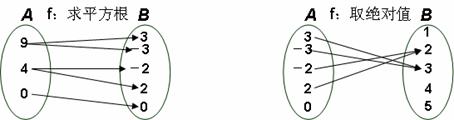 6.如下图所示对应关系
6.如下图所示对应关系 是从
是从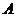 到
到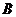 的映射的是 ( )
的映射的是 ( )
A.
B.
C. D.
7.若函数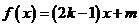 (
(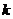 ,
,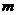 为常数)在区间
为常数)在区间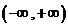 上是减函数,则有( )
上是减函数,则有( )
A.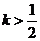 B.
B.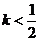 C.
C.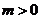 D.
D.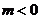
8.设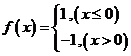 ,则不等式
,则不等式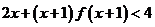 的解集是( )
的解集是( )
A.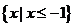 B.
B.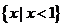 C.
C.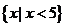 D.
D.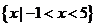
9.已知函数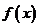 是在定义域
是在定义域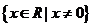 上的奇函数,当
上的奇函数,当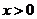 时,
时,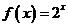 ,则当
,则当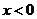 时,
时,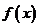 的解析式是
( )
的解析式是
( )
A.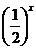 B.
B.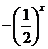 C.
C.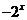 D.
D.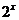
10.如果集合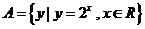 ,
,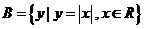 ,那么 ( )
,那么 ( )
A.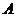
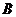 B.
B.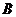
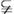
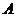 C.
C.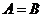 D.
D.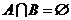
11.函数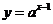 (
(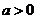 ,且
,且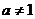 )与
)与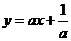 在同一直角坐标中的图像可能是
( )
在同一直角坐标中的图像可能是
( )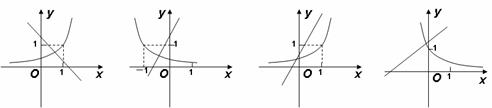
 A.
B.
C.
D.
A.
B.
C.
D.
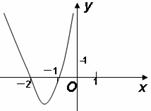
12.已知函数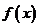 是
是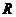 上的奇函数,且当
上的奇函数,且当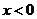 时,函数的部分图像如图所示,则不等式
时,函数的部分图像如图所示,则不等式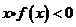 的解集是( )
的解集是( )
A.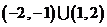 B.
B.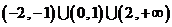
C.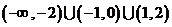 D.
D.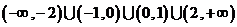
Ⅱ卷
13.若函数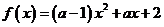 是偶函数,则函数
是偶函数,则函数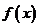 单调增函数区间是
单调增函数区间是
14.已知集合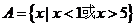 ,
,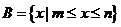 ,且
,且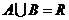 ,
,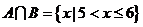 ,则
,则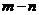
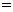
15.若函数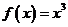 在区间
在区间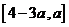 上是奇函数,则
上是奇函数,则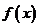 在区间
在区间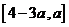 的最小值是
(用具体数字作答)
的最小值是
(用具体数字作答)
16.设函数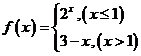 ,则方程
,则方程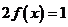 的解集是
的解集是
17.(本小题12分)设全集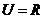 ,
,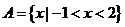 ,
,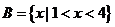 ,求
,求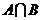 ,
,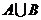 ,
,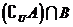 .
.
18.(本小题12分)判断各组函数是否表示同一函数,并且简要说明理由.
(1)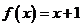 与
与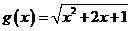 ;
;
(2)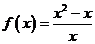 与
与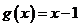 ;
;
(3)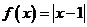 与
与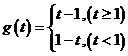 .
.
19.(本小题12分)若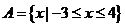 ,
,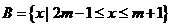 ,且
,且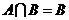 ,试求实数
,试求实数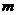 的取值范围.
的取值范围.
20.(本小题12分)已知函数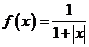 .
.
(1)判断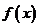 的奇偶性;
的奇偶性;
(2)确定函数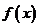 在
在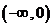 上是增函数还是减函数?证明你的结论.
上是增函数还是减函数?证明你的结论.
21.(本小题12分)设函数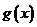 是定义在
是定义在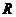 上的奇函数,
上的奇函数,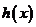 定义在
定义在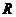 上的偶函数,并且
上的偶函数,并且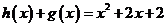 .
.
(1)求函数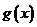 ,
,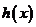 的解析式;
的解析式;
(2)令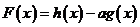 (
(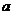 为常数),求
为常数),求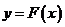 在区间
在区间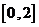 上的最小值.
上的最小值.
22.(本小题14分)设函数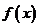 为一次函数.
为一次函数.
(1)若方程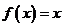 有唯一解
有唯一解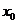 ,则称点
,则称点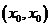 迭代不动点,试求函数
迭代不动点,试求函数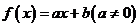 的迭代不动点;
的迭代不动点;
(2) 函数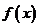 满足:
满足: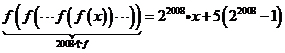 .求
.求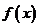 .
.

