1.设复数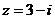 ,则
,则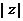 = ▲ .
= ▲ .
2.已知函数 的定义域为集合
的定义域为集合 ,
,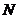 为自然数集,则
为自然数集,则 = ▲ .
= ▲ .
3.直线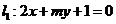 与直线
与直线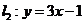 平行的充要条件是
平行的充要条件是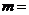 ▲ .
▲ .
 4.执行如图所示的伪代码,输出的结果是 ▲ .
4.执行如图所示的伪代码,输出的结果是 ▲ .
5.某几何体的三视图如图所示,主视图与左视图中两矩形的长和宽分别为4与2,俯视图中两同心圆的直径分别为4与2,则该几何体的体积等于 ▲ .
6.双曲线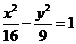 的顶点到它的渐近线的距离为 ▲ .
的顶点到它的渐近线的距离为 ▲ .
7.已知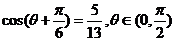 ,则
,则 = ▲ .
= ▲ .
8.已知 之间的一组数据如下表:
之间的一组数据如下表:
x
2
3
4
5
6
y
3
4
6
8
9
对于表中数据,现给出如下拟合直线:①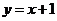 、②
、②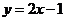 、③
、③ 、④
、④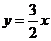 ,则根据最小二乘思想得拟合程度最好的直线是 ▲ (填序号).
,则根据最小二乘思想得拟合程度最好的直线是 ▲ (填序号).
10.国际上钻石的重量计量单位为克拉.已知某
种钻石的价值V(美元)与其重量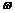 (克拉)
(克拉)
的平方成正比,若把一颗钻石切割成重量
分别为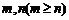 的两颗钻石,且价值损失的
的两颗钻石,且价值损失的
百分率=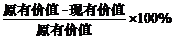 (切割中
(切割中
重量损耗不计),则价值损失的百分率的最大值
为 ▲ .
11.如图所示的三角形数阵中,满足:(1)第1行的数为1;(2)第n(n≥2)行首尾两数均为n,其余的数都等于它肩上的两个数相加,则第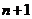 行中第2个数是 ▲ (用n表示).
行中第2个数是 ▲ (用n表示).
12.已知函数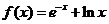 (
(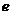 是自然对数的底数),若实数
是自然对数的底数),若实数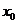 是方程
是方程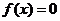 的解,且
的解,且 ,则
,则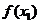 ▲
▲ 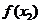 (填“>”,“≥”,“<”,“≤”).
(填“>”,“≥”,“<”,“≤”).
13.已知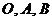 是平面上不共线三点,设
是平面上不共线三点,设 为线段
为线段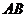 垂直平分线上任意一点,若
垂直平分线上任意一点,若 ,
,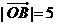 ,则
,则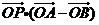 的值为 ▲ .
的值为 ▲ .
14. 已知关于x的方程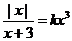 有三个不同的实数解,则实数k的取值范围是 ▲ .
有三个不同的实数解,则实数k的取值范围是 ▲ .
15.(本小题满分14分)
等可能地取点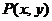 ,其中
,其中 .
.
(Ⅰ)当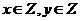 时,求点
时,求点 满足
满足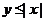 的概率;
的概率;
(Ⅱ)当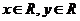 时,求点
时,求点 满足
满足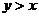 的概率.
的概率.
16.(本小题满分14分)
如图,在直三棱柱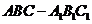 中,
中, ,
,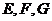 分别是
分别是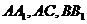 的中点,且
的中点,且 .
.
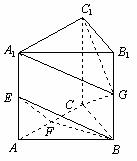 (Ⅰ)求证:
(Ⅰ)求证: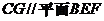 ;
;
(Ⅱ)求证: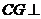 平面
平面 .
.
17.(本小题满分14分)
已知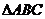 的三个内角
的三个内角 所对的边分别为
所对的边分别为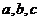 ,且
,且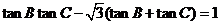 .
.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)现给出三个条件:①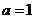 ;②
;②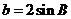 ;③
;③ .
.
试从中选择两个条件求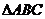 的面积(注:只需选择一个方案答题,如果用多种方案答题,则按第一种方案给分).
的面积(注:只需选择一个方案答题,如果用多种方案答题,则按第一种方案给分).
18.(本小题满分16分)
已知椭圆 的右焦点为F,右准线为
的右焦点为F,右准线为 ,且直线
,且直线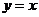 与
与 相交于A点.
相交于A点.
(Ⅰ)若⊙C经过O、F、A三点,求⊙C的方程;
(Ⅱ)当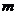 变化时, 求证:⊙C经过除原点O外的另一个定点B;
变化时, 求证:⊙C经过除原点O外的另一个定点B;
(Ⅲ)若 时,求椭圆离心率
时,求椭圆离心率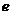 的范围.
的范围.
19.(本小题满分16分)
设首项为 的正项数列
的正项数列 的前
的前 项和为
项和为 ,
, 为非零常数,已知对任意正整数
为非零常数,已知对任意正整数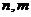 ,
,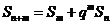 总成立.
总成立.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)若不等的正整数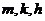 成等差数列,试比较
成等差数列,试比较 与
与 的大小;
的大小;
(Ⅲ)若不等的正整数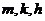 成等比数列,试比较
成等比数列,试比较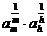 与
与 的大小.
的大小.
20.(本小题满分16分)
已知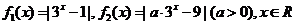 ,
,
且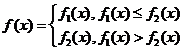 .
.
(Ⅰ)当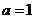 时,求
时,求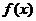 在
在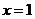 处的切线方程;
处的切线方程;
(Ⅱ)当 时,设
时,设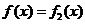 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为 (闭区间
(闭区间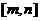 的长度定义为
的长度定义为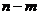 ),试求
),试求 的最大值;
的最大值;
(Ⅲ)是否存在这样的 ,使得当
,使得当 时,
时,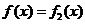 ?若存在,求出
?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
盐城市2008/2009学年度高三年级第二次调研

 9.数列
9.数列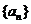 满足
满足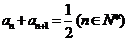
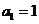 ,
,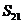 = ▲ .
= ▲ .