 1、已知集合
1、已知集合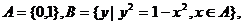 则
则 =
( )
=
( )
 A.
A. B.
B. 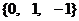 C.
C.
 D.
D. 
 2、设条件
2、设条件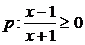 ;条件
;条件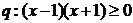 ,则
,则 是
是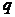 的
(
)
的
(
)
 A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
 3、
3、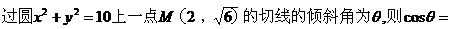 (
)
(
)
 A、
A、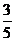 B、-
B、-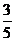 C、
C、 D、-
D、-
 4、已知直线
4、已知直线 、
、 ,平面
,平面 ,则下列命题中假命题是
( )
,则下列命题中假命题是
( )
 A.若
A.若 ,
,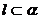 ,则
,则 B.若
B.若 ,
, ,则
,则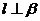
 C.若
C.若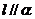 ,
, ,则
,则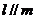 D.若
D.若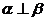 ,
,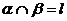 ,
, ,
, ,则
,则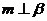
 5、
5、 ( )
( )
 A、
A、 B、
B、 C、
C、 D、
D、
 6、若不等式组
6、若不等式组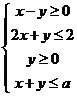 ,表示的平面区域是一个三角形区域,则
,表示的平面区域是一个三角形区域,则 的取值范围是 ( )
的取值范围是 ( )
 A.
A.
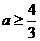 B.
B.  C.
C.
 D.
D.
 或
或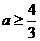
 7、
7、
 ( )
( )
 A、
A、 B、
B、 C、
C、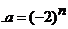 D、
D、
 8、对于区间
8、对于区间 上有意义的两个函数
上有意义的两个函数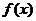 与
与 ,如果对于区间
,如果对于区间 中的任意数
中的任意数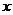 均有
均有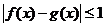 ,则称函数
,则称函数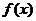 与
与 在区间
在区间 上是密切函数,
上是密切函数, 称为密切区间.若
称为密切区间.若 与
与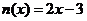 在某个区间上是“密切函数”,则它的一个密切区间可能是( )
在某个区间上是“密切函数”,则它的一个密切区间可能是( )
 A.
A.
 B.
B. 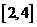 C.
C.
 D.
D.

 9、
9、
 10、某人5次下班途中所花的时间(单位:分钟)分别为m,n,5,6,4。已知这组数据的平均数为5,方差为2,则?m-n?的值为
. 4
10、某人5次下班途中所花的时间(单位:分钟)分别为m,n,5,6,4。已知这组数据的平均数为5,方差为2,则?m-n?的值为
. 4
 11、
11、
 ――――――
――――――
 12、已知数列{an}的前三项依次是-2,2,6,前n项和Sn是n的二次函数,则a100=_______
12、已知数列{an}的前三项依次是-2,2,6,前n项和Sn是n的二次函数,则a100=_______
 13、将有编号的7个球全部投入到甲、乙两个盒子中,每个盒子中至少投入2个球,那么不同的投入方法有
13、将有编号的7个球全部投入到甲、乙两个盒子中,每个盒子中至少投入2个球,那么不同的投入方法有
 (用数字作答)
(用数字作答)
 14、已知过球面上A,B,C三点的截面和球心的距离是球直径的
14、已知过球面上A,B,C三点的截面和球心的距离是球直径的 ,且
,且 则该球的表面积为
.
则该球的表面积为
.
 其中正确命题的序号是____________ (把你认为正确的都填上)
其中正确命题的序号是____________ (把你认为正确的都填上)
 17、(本小题满分12分)
17、(本小题满分12分)
 某高等学校自愿献血的50位学生的血型分布的情况如下表:
某高等学校自愿献血的50位学生的血型分布的情况如下表:

血型
A
B
AB
O
人数
20
10
5
15
 (Ⅰ)从这50位学生中随机选出2人,求这2人血型都为A型的概率;
(Ⅰ)从这50位学生中随机选出2人,求这2人血型都为A型的概率;
 (Ⅱ)从这50位学生中随机选出2人,求这2人血型相同的概率;
(Ⅱ)从这50位学生中随机选出2人,求这2人血型相同的概率;
 18、(本小题满分12分)
18、(本小题满分12分)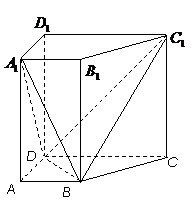
 如图,已知在直四棱柱
如图,已知在直四棱柱 中,
中, ,
,

 ,
,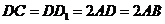
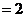 .
.
 (I)求证:
(I)求证: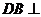 平面
平面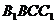 ;
;
 (II)求二面角
(II)求二面角 的余弦值.
的余弦值.
 19、(本小题满分13分)
19、(本小题满分13分)
 对于数列
对于数列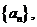 定义数列
定义数列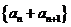 为
为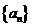 的“和数列”
的“和数列”
 (1)若
(1)若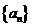 的“和数列”的通项为2n+1,
的“和数列”的通项为2n+1,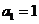 ,求
,求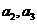 ,并写出
,并写出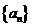 的通项公式。(不必证明)
的通项公式。(不必证明)
 (2)若
(2)若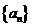 的“和数列”的通项为
的“和数列”的通项为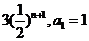 ,数列
,数列 满足
满足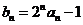 ,求
,求
 21、 (本小题满分13分)
21、 (本小题满分13分)
 设函数
设函数 (
( >0)
>0)
 (Ⅰ)若
(Ⅰ)若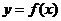 在
在 时,有极值
时,有极值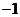 ,求
,求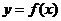 的单调区间。
的单调区间。
 (Ⅱ)证明:
(Ⅱ)证明: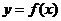 的图像上存在着与直线
的图像上存在着与直线 垂直的切线。
垂直的切线。
 (Ⅲ)若
(Ⅲ)若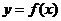 在
在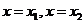 处取得极值,且
处取得极值,且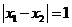 ,求b的取值范围。
,求b的取值范围。

湖南省2009届高三 十二校联考 第二次考试
 数学试卷(文科)
数学试卷(文科)
 总分:150分 时量:120分钟
总分:150分 时量:120分钟

|

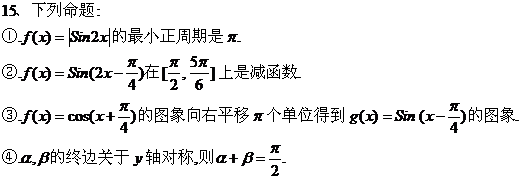



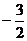
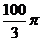
 …………………….3分
…………………….3分
 …………………….6分
…………………….6分
 ……………………10分
……………………10分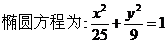 ……………………12分
……………………12分 ,
,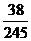 .
┅┅┅┅6分
.
┅┅┅┅6分 ,
, .
┅┅┅┅12分
.
┅┅┅┅12分 是
是 的中点,连结
的中点,连结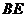 ,则四边形
,则四边形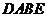 为正方形,
为正方形,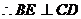 .故
.故 ,
, ,
,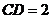 ,
, ,即
,即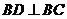 . ………3分
. ………3分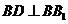 ,
, ………4分
………4分
 平面
平面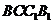 ,
………5分
,
………5分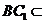 平面
平面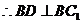 ,
,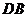 的中点
的中点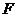 , 连结
, 连结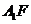 ,又
,又 ,则
,则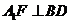 .
.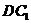 的中点
的中点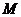 ,连结
,连结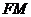 ,则
,则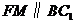 ,
,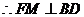 .
. 为二面角
为二面角 ,在
,在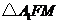 中,
中,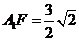 ,
,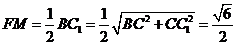 ,
, 的中点
的中点 ,连结
,连结 ,
, ,
,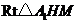 中,
中,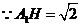 ,
,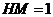 ,
, .
……….10分
.
……….10分 .
.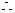 二面角
二面角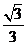 .
………..12分
.
………..12分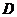 为原点,
为原点,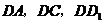 所在直线分别为
所在直线分别为 轴,
轴,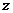 轴建立如图所示的空间直角坐标系,则
轴建立如图所示的空间直角坐标系,则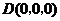 ,
,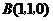 ,
,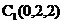 ,
, ,
,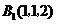 ,
,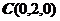 .
………..2分
.
………..2分
 ,
,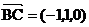 ,
,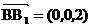 ………..3分
………..3分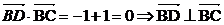
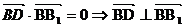
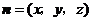 为平面
为平面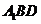 的一个法向量.
的一个法向量. ,
, ,
,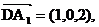
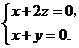 取
取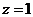 ,则
,则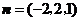 .
………..7分
.
………..7分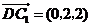 ,
, 为平面
为平面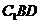 的一个法向量,
的一个法向量, ,
, ,得
,得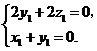 取
取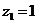 ,则
,则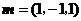 ,
………..9分
,
………..9分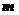 与
与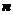 的夹角为
的夹角为 ,二面角
,二面角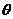 ,显然
,显然 ,
………..12分
,
………..12分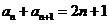
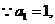 ,令
,令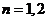 ,求得
,求得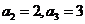 ………………………………2分
………………………………2分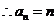 …………………………………………………………5分
…………………………………………………………5分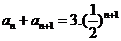
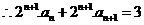 ………………
……………… ………………7分
………………7分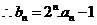
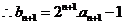 ………………8分
………………8分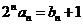
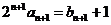 代入
代入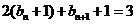
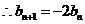 ………………10分
………………10分
 是以1为首项,-2为公比的等比数列。
是以1为首项,-2为公比的等比数列。
 ………………13分
………………13分
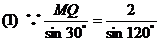
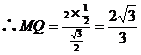 ………………2分
………………2分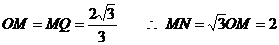 ………………4分
………………4分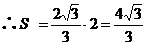 ………………5分
………………5分
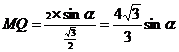


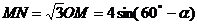 ………………7分
………………7分
 (
(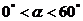 )
………………8分
)
………………8分 ………………11分
………………11分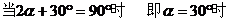 ,
, ………………13分
………………13分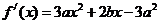
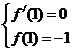 即
即 …………………………1分
…………………………1分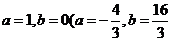 舍去)
………………………………………2分
舍去)
………………………………………2分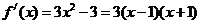
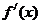 >0得
>0得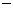 1
1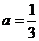 时,直线
时,直线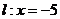 ,则
,则 >0恒成立,方程有解。
……………………5分
>0恒成立,方程有解。
……………………5分
 时,直线
时,直线 ,则与
,则与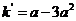
 即
即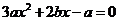
 >0恒成立,方程有解。
>0恒成立,方程有解。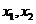 为
为 的两根
的两根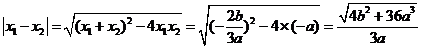 ………………8分
………………8分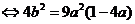 ………………………………………………9分
………………………………………………9分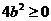 得 0<
得 0<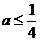 ………………………………………………………………10分
………………………………………………………………10分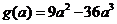

 则
则 ……………………………………………………………11分
……………………………………………………………11分 在
在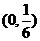 递增,
递增, 递减, 从而
递减, 从而 上的极大值为
上的极大值为
 ,且最小值为0,则
,且最小值为0,则
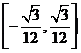 ………………………………………………13分
………………………………………………13分