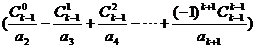1.如果复数 的模为
的模为 ,则
,则 6 .
6 .
2.已知集合 ,则
,则
 .
.
3.抛物线 的焦点坐标为
的焦点坐标为  .
.
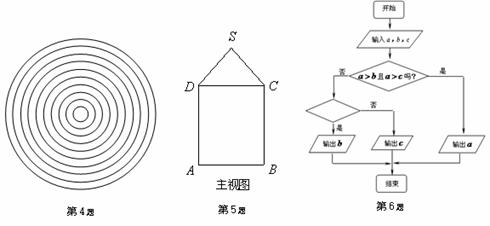
4.如图所示,一个水平放置的“靶子”共由10个同心圆构成,其半径分别为1┩、2┩、3┩、…、10┩,最内的小圆称为10环区,然后从内向外的圆环依次为9环区、8环区、…、1环区,现随机地向“靶子”上撒一粒豆子,则豆子落在8环区的概率为  .
.
5.某几何体的底部为圆柱,顶部为圆锥,其主视图如图所示,若 ,则该几何体的体积为
,则该几何体的体积为  .
.
6.如图所示的程序框图,如果输入三个实数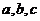 ,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入的内容是
,要求输出这三个数中最大的数,那么在空白的判断框中,应该填入的内容是  .
.
7.将函数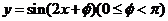 的图象向左平移
的图象向左平移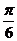 个单位后,所得的函数恰好是偶函数,则
个单位后,所得的函数恰好是偶函数,则 的值为
的值为 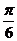 .
.
8.已知函数 ,数列
,数列 满足
满足 ,且数列
,且数列 是递增数列,则实数
是递增数列,则实数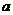 的取值范围是 (2,3) .
的取值范围是 (2,3) .
 9.图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第
9.图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第 个图形包含
个图形包含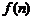 个“福娃迎迎”,则
个“福娃迎迎”,则
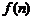 =
=  .(答案用数字或
.(答案用数字或 的解析式表示)
的解析式表示)
10.已知递增的等比数列 满足
满足 ,且
,且 的等差中项,若
的等差中项,若 ,则数列
,则数列 的前
的前 项和
项和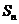 =
=  .
.
11.在边长为1的菱形 中,
中,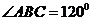 ,E、F分别是BC、CD的中点,DE交AF于点H ,则
,E、F分别是BC、CD的中点,DE交AF于点H ,则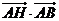 =
=  .
.
12.若关于 的方程
的方程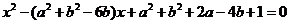 的两个实数根
的两个实数根 满足
满足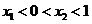 ,则
,则 的取值范围是
的取值范围是  .
.
13.若椭圆 上任一点到其上顶点的最大距离恰好等于该椭圆的中心到其准线的距离,则该椭圆的离心率的取值范围是
上任一点到其上顶点的最大距离恰好等于该椭圆的中心到其准线的距离,则该椭圆的离心率的取值范围是  .
.
14.已知定义在R上的函数 满足
满足 ,当
,当 时,
时, . 若对任意的
. 若对任意的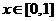 ,不等式组
,不等式组 均成立,则实数k的取值范围是
均成立,则实数k的取值范围是 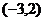 .
.
第II卷(解答题)
15.(本小题满分14分)
如图所示,角 为钝角,且
为钝角,且 ,点
,点 分别在角
分别在角 的两边上.
的两边上.
(Ⅰ)若 ,求
,求 的长;
的长;
(Ⅱ)设 ,且
,且 ,求
,求 的值.
的值.
解:(Ⅰ)因为角 为钝角,且
为钝角,且 ,所以
,所以 …………………………2分
…………………………2分
在 中,由
中,由 ,
,
得 ………………………………………………5分
………………………………………………5分
解得 或
或 (舍),即
(舍),即 的长为2………………………………………7分
的长为2………………………………………7分
(Ⅱ)由 ,得
,得 …………………………………………………9分
…………………………………………………9分
又 ,
,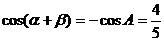 ………………………………11分
………………………………11分
所以
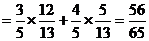 ……………………………………………………………………14分
……………………………………………………………………14分
16.(本小题满分14分)
 某高中地处县城,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
某高中地处县城,学校规定家到学校的路程在10里以内的学生可以走读,因交通便利,所以走读生人数很多.该校学生会先后5次对走读生的午休情况作了统计,得到如下资料:
①
若把家到学校的距离分为五个区间: ,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
,则调查数据表明午休的走读生分布在各个区间内的频率相对稳定,得到了如右图所示的频率分布直方图;
② 走读生是否午休与下午开始上课的时间有着密切的关系. 下表是根据5次调查数据得到的下午开始上课时间与平均每天午休的走读生人数的统计表.
下午开始上课时间
1:30
1:40
1:50
2:00
2:10
平均每天午休人数
250
350
500
650
750
(Ⅰ)若随机地调查一位午休的走读生,其家到学校的路程(单位:里)在 的概率是多少?
的概率是多少?
(Ⅱ)如果把下午开始上课时间1:30作为横坐标0,然后上课时间每推迟10分钟,横坐标x增加1,并以平均每天午休人数作为纵坐标y,试根据表中的5列数据求平均每天午休人数 与上课时间x之间的线性回归方程
与上课时间x之间的线性回归方程 ;
;
(Ⅲ)预测当下午上课时间推迟到2:20时,家距学校的路程在6里路以上的走读生中约有多少人午休?
解答:(Ⅰ)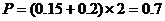 …………………………………………………4分
…………………………………………………4分
(Ⅱ)根据题意,可得如下表格:
x
0
1
2
3
4
y
250
350
500
650
750
则
所以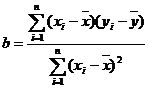
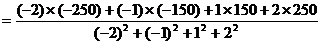
 ………8分
………8分
再由 ,得
,得 ,故所求线性回归方程为
,故所求线性回归方程为 ……………………10分
……………………10分
(Ⅲ)下午上课时间推迟到2:20时, ,
, ,
,
此时,家距学校的路程在6里路以上的走读生中约有133人(134人)……………………14分
17.(本小题满分14分)如图甲,在直角梯形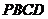 中,
中, ,
, ,
, ,
, 是
是 的中点. 现沿
的中点. 现沿 把平面
把平面 折起,使得
折起,使得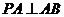 (如图乙所示),
(如图乙所示),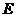 、
、 分别为
分别为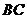 、
、 边的中点.
边的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面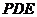 ;
;
(Ⅲ)在 上找一点
上找一点 ,使得
,使得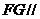 平面
平面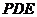 .
.
解答:(Ⅰ)证:因为PA⊥AD,PA⊥AB, ,所以
,所以 平面
平面 ……………4分
……………4分
(Ⅱ)证:因为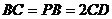 ,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由
,A是PB的中点,所以ABCD是矩形,又E为BC边的中点,所以AE⊥ED。又由 平面
平面 ,得
,得
 ,且
,且 ,所以
,所以 平面
平面 ,而
,而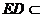 平面
平面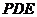 ,故平面
,故平面 平面
平面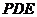 …………………………………………………………9分
…………………………………………………………9分
(Ⅲ)过点 作
作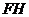 ∥
∥ 交
交 于
于 ,再过
,再过 作
作 ∥
∥ 交
交 于
于 ,连结
,连结 。
。
由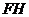 ∥
∥ ,
,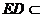 平面
平面 ,得
,得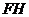 ∥平面
∥平面 ;
;
由 ∥
∥ ,
,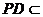 平面
平面 ,得
,得 ∥平面
∥平面 ,
,
又 ,所以平面
,所以平面 ∥平面
∥平面 ……………………………………………12分
……………………………………………12分
再分别取 、
、 的中点
的中点 、
、 ,连结
,连结 、
、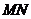 ,易知
,易知 是
是 的中点,
的中点, 是
是 的中点,从而当点
的中点,从而当点 满足
满足 时,有
时,有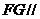 平面
平面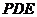 。………………………………………14分
。………………………………………14分
18.(本小题满分16分)
已知圆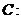
 ,相互垂直的两条直线
,相互垂直的两条直线 、
、 都过点
都过点 .
.
(Ⅰ)若 、
、 都和圆
都和圆 相切,求直线
相切,求直线 、
、 的方程;
的方程;
(Ⅱ)当 时,若圆心为
时,若圆心为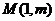 的圆和圆
的圆和圆 外切且与直线
外切且与直线 、
、 都相切,求圆
都相切,求圆 的方程;
的方程;
(Ⅲ)当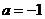 时,求
时,求 、
、 被圆
被圆 所截得弦长之和的最大值.
所截得弦长之和的最大值.
解答:(Ⅰ)显然,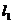 、
、 的斜率都是存在的,设
的斜率都是存在的,设 ,则
,则
……………………………………………………………………………………………1分
则由题意,得 ,
, ………………………………………………3分
………………………………………………3分
解得 且
且 ,即
,即 且
且 ……………………………5分
……………………………5分
∴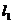 、
、 的方程分别为
的方程分别为 与
与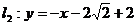 或
或 与
与 ……………………………………………………………………………6分
……………………………………………………………………………6分
(Ⅱ)设圆 的半径为
的半径为 ,易知圆心
,易知圆心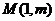 到点
到点 的距离为
的距离为 ,
,
∴ ………………………………………………………9分
………………………………………………………9分
解得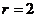 且
且 ,∴圆
,∴圆 的方程为
的方程为 ………………………11分
………………………11分
(Ⅲ)当 时,设圆
时,设圆 的圆心为
的圆心为 ,
,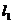 、
、 被圆
被圆 所截得弦的中点分别为
所截得弦的中点分别为 ,弦长分别为
,弦长分别为 ,因为四边形
,因为四边形 是矩形,所以
是矩形,所以 ,即
,即
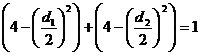 ,化简得
,化简得 …………………………………14分
…………………………………14分
从而 ,
,
即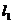 、
、 被圆
被圆 所截得弦长之和的最大值为
所截得弦长之和的最大值为 …………………………………16分
…………………………………16分
19.(本小题满分16分)
设函数 .
.
(Ⅰ)求证:当 时,
时,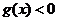 ;
;
(Ⅱ)存在 ,使得
,使得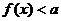 成立,求
成立,求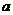 的取值范围;
的取值范围;
(Ⅲ)若 对
对 恒成立,求
恒成立,求 的取值范围.
的取值范围.
解答:(Ⅰ)解答:(Ⅰ)因为当 时,
时, ,
,
所以 在
在 上单调递减,………………………………………………………3分
上单调递减,………………………………………………………3分
又 ,所以当
,所以当 时,
时, ……………………………………………4分
……………………………………………4分
(Ⅱ) 因为 ,所以
,所以 ,
,
由(Ⅰ)知,当 时,
时,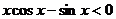 ,所以
,所以 ………………………6分
………………………6分
所以 在
在 上单调递减,则当
上单调递减,则当 时,
时,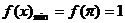 ………………………8分
………………………8分
由题意知,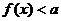 在
在 上有解,所以
上有解,所以 ,从而
,从而 ………………………10分
………………………10分
(Ⅲ)由
 得
得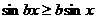
 对
对 恒成立,
恒成立,
①当 时,不等式显然成立………………………………………………………11分
时,不等式显然成立………………………………………………………11分
②当 时,因为
时,因为 ,所以取
,所以取 ,则有
,则有 ,从而此时不等式不恒成立…………………………………………………………………………12分
,从而此时不等式不恒成立…………………………………………………………………………12分
③当 时,由(Ⅱ)可知
时,由(Ⅱ)可知 在
在 上单调递减,而
上单调递减,而 ,
,
∴ , ∴
, ∴ 成立………………………………………14分
成立………………………………………14分
④当 时,当
时,当 时,
时, ,则
,则
 ,∴
,∴ 不成立,
不成立,
综上所述,当 或
或 时,有
时,有 对
对 恒成立。
恒成立。
………………………………………………………………………………………………16分
20.(本小题满分16分)
数列 满足
满足 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)当 为某等差数列的第1项,第
为某等差数列的第1项,第 项,第
项,第 +7项,且
+7项,且 ,求
,求 与
与 ;
;
(Ⅲ)求证:数列 中能抽取出一个子数列成等比数列
中能抽取出一个子数列成等比数列 的充要条件是
的充要条件是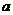 为有理数.
为有理数.
解答:(Ⅰ)当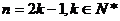 时,
时, ,∴
,∴ ……2分
……2分
当 时,
时, ,∴
,∴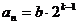 …………………………………………4分
…………………………………………4分
∴

 …………………………………………5分
…………………………………………5分
(Ⅱ)当 时,
时, ,则该等差数列的公差为
,则该等差数列的公差为
 ,∴
,∴ ,
,
即 ①
①
又 ,所以
,所以 ,即
,即 ②
②
由①知, 为整数或分母为7的既约分数;由②知,
为整数或分母为7的既约分数;由②知, 为整数或分母为2的既约分数,从而
为整数或分母为2的既约分数,从而 必为整数………………………………………………………………………7分
必为整数………………………………………………………………………7分
由②知, ,结合①得,
,结合①得,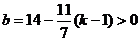 ,所以
,所以 只能取7,故
只能取7,故 ,………8分
,………8分
又由②得,
 ,设
,设
则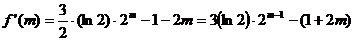 ,
,
因为

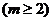
所以当 时,
时, ,又
,又 ,
,
从而 ,故
,故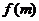 在
在 上单调递增。
上单调递增。
则由 ,知
,知 在
在 上无解…………………………10分
上无解…………………………10分
又 ,
, ,
, ,
,
所以 或
或 ,
,
综上所述,当 ,且
,且 或
或 时满足条件……………………………………………11分
时满足条件……………………………………………11分
(Ⅲ)①必要性。若 中存在一个子数列
中存在一个子数列 成等比数列,设
成等比数列,设 为其中的连续三项。因为
为其中的连续三项。因为 ,所以
,所以 ,则
,则
 ……………………………………………………12分
……………………………………………………12分
⑴当 时,
时, ,即
,即 ,则
,则 ,矛盾;
,矛盾;
⑵当 时,
时, ,则
,则 ,所以必要性成立………………13分
,所以必要性成立………………13分
②充分性。若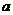 为有理数,因为
为有理数,因为 ,所以可取足够大的正整数
,所以可取足够大的正整数 ,使
,使
 ,因为
,因为 也为有理数,故可设
也为有理数,故可设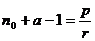 (其中
(其中 为互质正整数)。
为互质正整数)。
现构造等比数列 ,使得首项
,使得首项 ,公比
,公比 ,则
,则
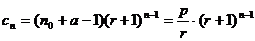 …………………………………………14分
…………………………………………14分
因为 ,
,
所以 ,
,
从而 ,
,
设 ,则
,则 为正整数,
为正整数,
则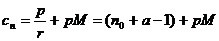
 ,故
,故 必为
必为 中的项,即等比数列
中的项,即等比数列 是
是 的子数列,所以充分性也成立。
的子数列,所以充分性也成立。
综合①②知,原命题成立。……………………………………………………………………16分
数学附加题
21.[选做题] 在A、B、C、D四小题中只能选做2题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
A.(选修4―1:几何证明选讲)
如图,四边形ABCD内接于圆 ,弧
,弧 弧
弧 ,过A点的切线交CB的延长线于E点.
,过A点的切线交CB的延长线于E点.
 求证:
求证: .
.
证:连结 ,因为
,因为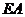 切圆
切圆 于
于 ,所以∠EAB=∠ACB。
,所以∠EAB=∠ACB。
因为弧 弧
弧 ,所以∠ACD=∠ACB,AB=AD,于是∠EAB=∠ACD………………5分
,所以∠ACD=∠ACB,AB=AD,于是∠EAB=∠ACD………………5分
又四边形ABCD内接于圆 ,所以∠ABE=∠D,所以△ABE∽CDA.
,所以∠ABE=∠D,所以△ABE∽CDA.
于是 ,即
,即 ,所以
,所以 …………………………10分
…………………………10分
B.(选修4―2:矩阵与变换)
已知矩阵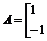
 ,A的一个特征值
,A的一个特征值 ,其对应的特征向量是
,其对应的特征向量是 .
.
(Ⅰ)求矩阵 ;
;
(Ⅱ)若向量 ,计算
,计算 的值.
的值.
解:(Ⅰ)
 ……………………………………………………………3分
……………………………………………………………3分
(Ⅱ)矩阵A的特征多项式为
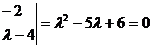 ,
,
解得 ……………………………………………………………6分
……………………………………………………………6分
当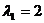 时,得
时,得 ;当
;当 时,得
时,得 ,
,
由 ,得
,得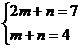 ,得
,得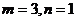 …………………………………8分
…………………………………8分
∴

 …………………………………………………10分
…………………………………………………10分
C.(选修4―4:坐标系与参数方程)
已知某圆的极坐标方程为ρ2 -4ρcos(θ-)+6=0.
(Ⅰ)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(Ⅱ)若点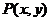 在该圆上,求
在该圆上,求 的最大值和最小值.
的最大值和最小值.
解答:(Ⅰ) ;
; (
( 为参数)……………5分
为参数)……………5分
(Ⅱ)因为 ,所以其最大值为6,最小值为2……………10分
,所以其最大值为6,最小值为2……………10分
D.(选修4―5:不等式选讲)
设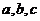 均为正实数.
均为正实数.
(Ⅰ)若 ,求
,求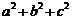 的最小值;
的最小值;
(Ⅱ)求证: .
.
解答:(Ⅰ)解:因为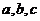 均为正实数,由柯西不等式得
均为正实数,由柯西不等式得
 ,当且仅当
,当且仅当 时等号成立,∴
时等号成立,∴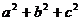 的最小值为
的最小值为 ………………………………………………5分
………………………………………………5分
(Ⅱ)∵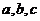 均为正实数,∴
均为正实数,∴ ,当
,当 时等号成立;
时等号成立;
则 ,当
,当 时等号成立;
时等号成立;
 ,当
,当 时等号成立;
时等号成立;
三个不等式相加得, ,当且仅当
,当且仅当 时等号成立。
时等号成立。
……………………………………………………………………10分
[必做题] 第22、23题,每小题10分,计20分.请把答案写在答题纸的指定区域内.
22.(本小题满分10分)
如图所示,已知曲线 ,曲线
,曲线  与
与 关于点
关于点 对称,且曲线
对称,且曲线 与
与 交于点O、A,直线
交于点O、A,直线 与曲线
与曲线 、
、 、
、 轴分别交于点
轴分别交于点 、
、 、
、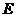 ,连结
,连结 .
.
 (Ⅰ)求曲边三角形
(Ⅰ)求曲边三角形 (阴影部分)的面积
(阴影部分)的面积 ;
;
(Ⅱ)求曲边三角形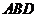 (阴影部分)的面积
(阴影部分)的面积 .
.
解答:(Ⅰ)易得曲线 的方程为
的方程为 …………………………………………2分
…………………………………………2分
由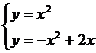 ,得点
,得点 ,又由已知得
,又由已知得 ………………4分
………………4分
故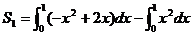
 ………………………………………6分
………………………………………6分
(Ⅱ) ………………………10分
………………………10分
23. (本小题满分10分)
已知 为等差数列,且
为等差数列,且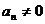 ,公差
,公差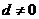 .
.
(Ⅰ)试证: ;
; ;
;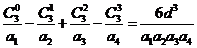 ;
;
(Ⅱ)根据(Ⅰ)中的几个等式,试归纳出更一般的结论,并用数学归纳法证明.
解答:(Ⅰ)略……………………………………………………………………3分
(Ⅱ)结论: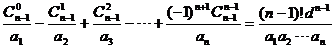 ………………………5分
………………………5分
证:①当 时,等式成立,
时,等式成立,
②假设当 时,
时, 成立,
成立,
那么当 时,因为
时,因为 ,所以
,所以



 ,
,
所以,当 时,结论也成立。
时,结论也成立。
综合①②知,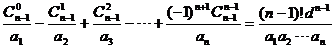 对
对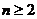 都成立…………10分
都成立…………10分
|