11.某工厂甲、乙、丙三条生产线共生产了某种产品180件,已知甲、乙、丙三条生产线各自生产的产品数依次组成一个等差数列. 为检查这批产品的质量,决定采用分层抽样的方法进行抽样,共抽取样品36件,则从乙生产线生产的产品中抽取了 件样品.
12. 正三棱锥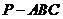 的底面边长为3,外接球的球心为
的底面边长为3,外接球的球心为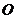 ,且
,且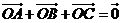 .则三棱锥
.则三棱锥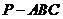 外接球的体积V= .
外接球的体积V= .
13. 已知椭圆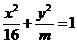 (m>0),若直线y=x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m=___________.
(m>0),若直线y=x与椭圆的一个交点M在x轴上的射影恰好是椭圆的右焦点F,则m=___________.
14. 平面内与直线垂直的非零向量称为直线的法向量,空间中与平面垂直的非零向量称为平面的法向量. 在平面直角坐标系中,直线的方程是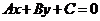 (A、B不同时为0),在空间直角坐标系中,平面的方程是
(A、B不同时为0),在空间直角坐标系中,平面的方程是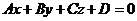 (A、B、C不同时为0). 利用求动点轨迹方程的方法,可以求出过点A(3,1)且法向量为
(A、B、C不同时为0). 利用求动点轨迹方程的方法,可以求出过点A(3,1)且法向量为 的直线(点法式)方程为
的直线(点法式)方程为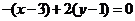 , 化简后得
, 化简后得 ;类比上述方法,在空间直角坐标系中,经过点A (2, 1, 3)
且法向量为
;类比上述方法,在空间直角坐标系中,经过点A (2, 1, 3)
且法向量为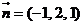 的平面(点法式)方程为 .(请写出化简后的结果)
的平面(点法式)方程为 .(请写出化简后的结果)
15. 给出下列命题:
① 已知 ,则p>q;
,则p>q;
② 函数 的图象关于直线
的图象关于直线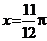 对称,在区间
对称,在区间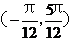 内是增函数;
内是增函数;
③ 函数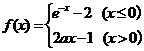 (a是常数且a>0)的最小值是-1, 且存在反函数;
(a是常数且a>0)的最小值是-1, 且存在反函数;
④ 在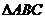 中,若AB=1,BC=2,则角C的取值范围是
中,若AB=1,BC=2,则角C的取值范围是 .
.
其中真命题的编号是 .(把你认为正确命题的序号都填上).
怀化市2008年高三第一次模拟考试统一检测试卷
 数学(理科)答题卷
数学(理科)答题卷
登 分 栏
题号
一
二
三
总分
16
17
18
19
20
21
得分
题号
1
2
3
4
5
6
7
8
9
10
答案
11、 ; 12、 ; 13、 ;
14、 ; 15、 .
评卷人
得 分
16、(本题满分12分)
已知锐角ΔABC中,角A、B、C的对边分别为a、b、c,且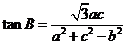 .
.
(I) 求角B的大小;
(II) 求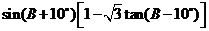 的值.
的值.
评卷人
得 分
17.(本小题满分12分)
 如图2,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC 所成的角为60°.
如图2,四边形PCBM是直角梯形,∠PCB=90°,PM∥BC,PM=1,BC=2,又AC=1,∠ACB=120°,AB⊥PC,直线AM与直线PC 所成的角为60°.
(Ⅰ)求证:平面PAC⊥平面ABC;
(Ⅱ)求二面角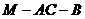 的大小.
的大小.
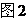 |
评卷人
得 分
评卷人
得 分
18. (本题满分12分)
某电视台《快乐五溪》节目有一个有奖竞猜的环节.主持人为幸运观众准备了A、B、C三个相互独立的问题,并且宣布:幸运观众答对问题A可获奖金1000元,答对问题B可获奖金2000元,答对问题C可获奖金4000元,回答问题的先后顺序由观众自由选择,且每种答题顺序的选择都是等可能的. 但只有第一个问题答对,才能再回答第二题,只有答对第二个问题,才能再回答第三题,否则终止答题.假设幸运观众能答对问题A、B、C的概率分别为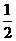 、
、 、
、 .
.
(I) 求幸运观众获得奖金5000元的概率;
(II)甲观众认为应选择先易后难的顺序(即A→B→C)回答问题,乙观众认为应选择先难后易的顺序(即C→B→A)回答问题. 请你分析他俩的说法,相比较而言,谁可能获得更多的奖金?
19.(本小题满分13分)
设函数 在
在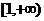 上是增函数.
上是增函数.
(Ⅰ)求正实数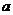 的取值范围;
的取值范围;
(Ⅱ)设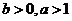 ,求证:
,求证: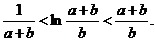
评卷人
得 分
20.(本小题满分13分)'
设不等式组 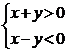 表示的平面区域为D,区域D内的动点P到直线
表示的平面区域为D,区域D内的动点P到直线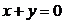 和直线
和直线 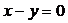 的距离之积为2, 记点P的轨迹为曲线C.
的距离之积为2, 记点P的轨迹为曲线C.
(Ⅰ)画图表示平面区域D,并求曲线C的方程;
(Ⅱ)是否存在过点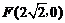 的直线l, 使之与曲线C交于相异两点
的直线l, 使之与曲线C交于相异两点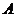 、
、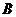 ,且以线段AB为直径的圆与y轴相切?若存在, 求出直线l的斜率;若不存在, 说明理由.
,且以线段AB为直径的圆与y轴相切?若存在, 求出直线l的斜率;若不存在, 说明理由.
评卷人
得 分
21.(本小题满分13分)
已知函数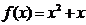 及正整数数列
及正整数数列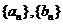 . 若
. 若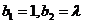 ,且当
,且当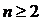 时,有
时,有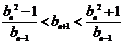 ; 又
; 又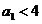 ,
,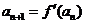 , 且对任意
, 且对任意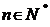 恒有
恒有 成立. 数列
成立. 数列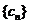 满足:
满足: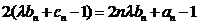 .
.
(Ⅰ) 求数列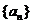 及
及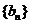 的通项公式;
的通项公式;
(Ⅱ) 求数列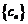 的前
的前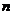 项和
项和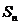 ;
;
(Ⅲ) 证明存在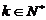 ,使得
,使得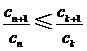 对任意
对任意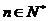 均成立.
均成立.
怀化市2008年高三第一次模拟考试统一检测试卷


