1. 是第四象限角,
是第四象限角, ,则
,则 ( )
( )
A. B.
B.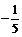 C.
C. D.
D.
A.66
B.
A.8或 2 B.6或
2 B.6或
 6 D.2或
6 D.2或 8
8
8.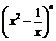 的展开式中,常数项为15,则
的展开式中,常数项为15,则 ( )
( )
A. B.
B. C.
C. D.
D.
 9.如图,ABCD―EFGH为边长等于1的立方体,若P点在立方体内部且满足
9.如图,ABCD―EFGH为边长等于1的立方体,若P点在立方体内部且满足 +
+ ,则P点到直线AB的距离为( )
,则P点到直线AB的距离为( )
A. B.
B. C.
C. D.
D.
10.若 的值为 ( )
的值为 ( )
A.-2 B.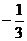 C.
C. D.3
D.3
11.设 均为正数,且
均为正数,且 ,
, ,
, .则( )
.则( )
A. B.
B. C.
C. D.
D.
12.设函数 ,则满足方程
,则满足方程 根的个数是( )
根的个数是( )
A. 1 个 B.2 个 C. 3 个 D.无数个
14.由数字0、1、2、3组成没有重复数字的正偶数,共有_________个.(用数字作答)
16. 给出下列命题中
① 非零向量 满足
满足 ,则
,则 的夹角为
的夹角为 ;
;
② 

 >0,是
>0,是 的夹角为锐角的充要条件;
的夹角为锐角的充要条件;
③ 将函数 的图象按向量
的图象按向量 平移,得到的图象对应的函数为
平移,得到的图象对应的函数为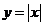 ;
;
④ 在 中,若
中,若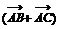
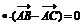 ,则
,则 为等腰三角形;
为等腰三角形;
以上命题正确的是
(注:把你认为正确的命题的序号都填上)
2008年甘肃省部分普通高中高三第一次联合考试
理科数学答题卷
13. 14. 15. 16.
17.(本题满分10分)
已知函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)求函数 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.
18.(本题满分12分)
某同学参加科普知识竞赛,需回答三个问题.竞赛规则规定:每题回答正确得100分,回答不正确得-100分.假设这名同学每题回答正确的概率均为0.8,且各题回答正确与否相互之间没有影响. 设这名同学回答这三个问题的总得分为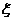 .
.
(Ⅰ)求这名同学总得分不为负分(即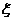 ≥0)的概率;
≥0)的概率;
(Ⅱ)求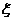 的概率分布和数学期望.
的概率分布和数学期望.
 (Ⅰ)求证:
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
20.(本题满分12分)
已知 、
、 为两个数列,其中
为两个数列,其中 是等差数列,且
是等差数列,且 .
.
(Ⅰ)求数列 的前n项和;
的前n项和;
(Ⅱ)若数列 满足
满足 求数列
求数列 的通项公式。
的通项公式。
21.(本题满分12分)
已知双曲线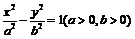 的离心率
的离心率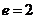 ,且B1、B2分别是双曲线虚轴的上、下端点.
,且B1、B2分别是双曲线虚轴的上、下端点.
(Ⅰ)若双曲线过点 ),求双曲线的方程;
),求双曲线的方程;
22. (本小题满分12分)
设函数
(1)求 的单调区间;
的单调区间;
(2)若当 时,(其中e=2.718…),不等式
时,(其中e=2.718…),不等式 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)若关于 的方程
的方程 在区间[0,2]上恰好有两个相异的实根,求实数
在区间[0,2]上恰好有两个相异的实根,求实数 的取值范围.
的取值范围.
2008年甘肃省部分普通高中高三第一次联合考试
理科数学答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
B
D
C
A
C
D
A
B
A
C
13. 14. 26 15. 5 16. ①③④
14. 26 15. 5 16. ①③④
17.(本题满分10分)本小题考查三角函数中的诱导公式、特殊角三角函数值、两角差公式、倍角公式、函数 的性质等基础知识,考查基本运算能力.满分10分.
的性质等基础知识,考查基本运算能力.满分10分.
(Ⅰ)解: .
.
因此,函数 的最小正周期为
的最小正周期为 .(4分)
.(4分)
(Ⅱ)法一: 在区间
在区间 上为增函数,在区间
上为增函数,在区间 上为减函数(7分),又
上为减函数(7分),又 ,
, ,
, ,
,

 故函数
故函数 在区间
在区间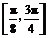 上的最大值为
上的最大值为 ,最小值为
,最小值为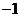 .(10分)
.(10分)
解法二:作函数 在长度为一个
在长度为一个
周期的区间 上的图象如下:(7分)
上的图象如下:(7分)
由图象得函数 在区间
在区间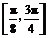 上的最大值为
上的最大值为 ,
,
最小值为 .(10分)
.(10分)
18、(本题满分12分)本小题主要考查离散型随机变量的分布列、数学期望等概念,以及运用概率统计知识解决实际问题的能力.满分12分.
解:(Ⅰ)这名同学总得分不为负分的概率为P(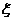 ≥0)= P(
≥0)= P(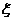 =100)+P(
=100)+P(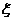 =300)=3×0.2×0.82
+0.83=0.384+0.512=0.896. (4分)
=300)=3×0.2×0.82
+0.83=0.384+0.512=0.896. (4分)
(Ⅱ)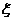 的可能值为-300,-100,100,300.
的可能值为-300,-100,100,300.
P(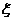 =-300)=0.23=0.008,
P(
=-300)=0.23=0.008,
P(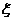 =-100)=3×0.22×0.8=0.096,
=-100)=3×0.22×0.8=0.096,
P(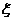 =100)=3×0.2×0.82=0.384,
P(
=100)=3×0.2×0.82=0.384,
P(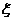 =300)=0.83=0.512,
=300)=0.83=0.512,
所以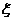 的概率分布为(8分)
的概率分布为(8分)

-300
-100
100
300
P
0.008
0.096
0.384
0.512
根据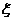 的概率分布,可得
的概率分布,可得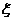 的期望
的期望
E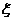 =(-300)×0.08+(-100)×0.096+100×0.384+300×0.512=180. (12分)
=(-300)×0.08+(-100)×0.096+100×0.384+300×0.512=180. (12分)
又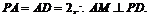
(Ⅱ)设平面AMN与PAB所成锐二面角的大小为 ,作
,作 ,则
,则 故所求平面AMN与PAB所成锐二面角的大小为
故所求平面AMN与PAB所成锐二面角的大小为 …………(12分)
…………(12分)
(Ⅰ)
又 ……………(7分)
……………(7分)
(Ⅱ)
|


 ,
, ,则数列
,则数列 等于( )
等于( ) ( )
( ) 则不等式
则不等式 的解集为( )
的解集为( ) B
B
 D
D
 则
则 ( )
( ) B
B C
C D
D
 =(1,
=(1,
 A
A



 则
则 的最小值是
的最小值是
 的底面是正方形,
的底面是正方形, ⊥底面
⊥底面 ,且
,且 ,点
,点 、
、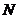 分别在侧棱
分别在侧棱 、
、 上,且
上,且
 ,求平面
,求平面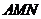 与平面
与平面 的所成锐二面角的大小
的所成锐二面角的大小 ,求直线AB的方程
,求直线AB的方程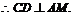
 又PA=AD=2,则有P(0,0,2),D(0,2,0)
又PA=AD=2,则有P(0,0,2),D(0,2,0)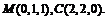

 ……………(3分)
……………(3分)
 即得
即得 ………………(9分)
………………(9分)




 ,条件中的等式可化为:
,条件中的等式可化为: , ①
, ① , ②
, ② …………10分
…………10分  时,
时, 得
得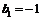 .
.
 ……………12分
……………12分
 ,
, ,又曲线C过点Q(2,
,又曲线C过点Q(2, ),
),
 ………………6分
………………6分 ,∴A、B2、B三点共线
,∴A、B2、B三点共线
 ,①
,① ②
② 代入双曲线方程得
代入双曲线方程得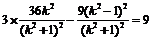 ,得
,得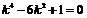 ,
, ,
, ………………14分
………………14分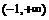 ,∵
,∵
 得x>0, 由
得x>0, 由 得-1<x<0,
得-1<x<0, 
 ,递减区间是
,递减区间是 (4分)
(4分) 得
得 由(1)知
由(1)知 上递减,在
上递减,在 上递增.
上递增. 所以
所以 故
故 时,不等式
时,不等式 恒成立; (8分)
恒成立; (8分) 记
记 ,
, .由
.由 得
得 由
由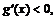 得
得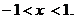
 在[0,1]上递减,在[1,2]上递增. (10分)
在[0,1]上递减,在[1,2]上递增. (10分) 在
在 上各有一个实根,于是有
上各有一个实根,于是有
 (12分)
(12分)