搜索
1．函数
(x>1)的反函数为y=
,则
等于 ……………………（ ）
A．3 B．
2．设集合
，
，则集合
的子集个数最多有（ ）
A．1个 B．2个 C．3个 D．4个
3． 从双曲线虚轴的一个端点看两个顶点的视角为直角，则双曲线的离心率为……… （ ）
A．
B．
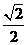D．
4．过P（1，1）作圆
的弦AB，若
，则AB的方程是………（ ）
A y=x+1
B.y=x +
5．在
展开式中，
的系数是 ………………………………………… （ ）
A． 
B． 
C．297
D．207
6．函数
的单调递增区间是 ………………………………………… （ ）
A．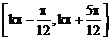
B． 
C．
D． 
7．若
，则b的取值范围是 ………………………………………… （ ）
A．
B． 
C．
D．
8．设
，则y=
的最小值为 ………………………………………… （ ）
A．24 B．
9．如图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形，现在用四种颜色给这四个直角三角形区域涂色，规定每个区域只涂一种颜色，相邻区域颜色不相同，则有多少种不同的涂色方法 ……………………………………………………………………………（ ）
A．24种 B．72种 C．84种 D．120种
10．平面
的一条斜线
与平面交于点P，Q是上一定点，过点Q的动直线
与垂直，那么与平面交点的轨迹是……… （ ）
A．直线 B. 圆 C. 椭圆 D. 抛物线
（第9题图）
得分
评卷人
复评人
11．
.
12．不等式
的解集为
．
13．设M是椭圆
上的动点，
和
分别是椭圆的左、右顶点，则
的
最小值等于 .
14.设
是定义在R上的奇函数，且
，
，则
．
15．将一个钢球置于由6根长度为m的钢管焊接成的正四面体的钢架内，那么，这个钢球的最大体积为 
.
得分
评卷人
复评人
16．（本小题满分12分）
已知
的外接圆的半径为
,内角A、B、C的对边分别为a、b、c，又向量
，
,且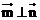
（I）求角C;
（II）求三角形ABC的面积S的最大值．
得分
评卷人
复评人
17．（本小题满分12分）
湖南省某单位从5名男职工和3名女职工中任意选派3人参加省总工会组织的“迎奥运，争奉献”演讲比赛．
（I）求该单位所派3名选手都是男职工的概率;
（II）求该单位男职工、女职工都有选手参加比赛的概率；
（III）如果参加演讲比赛的每一位选手获奖的概率均为
，则该单位至少有一名选手获奖的概率是多少？
得分
评卷人
复评人
18. （本小题满分12分）
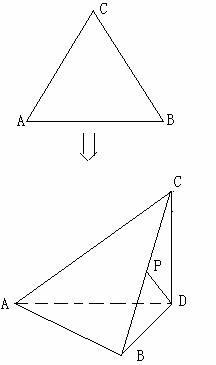
把边长为2的正三角形ABC沿BC上的高AD折成直二面角，设折叠后BC的中点为P.
（I）求异面直线AC，PD所成的角的余弦值;
（II）求二面角C―AB―D的大小;
（III）在AB上是否存在一点S，使得
？若存在，试确定S的位置，若不存在，试说明理由.
得分
评卷人
复评人
19．（本小题满分12分）
设函数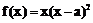
（I）证明：
是函数在区间
上递减的必要而不充分的条件；
（II）若
时，
恒成立，且
，求实数a的取值范围．
得分
评卷人
复评人
20．（本小题满分13分）
已知曲线C上的动点M到y轴的距离比到点F（1，0）的距离小1.
（I）求曲线C的方程;
（II）过F作弦PQ、RS，设PQ、RS的中点分别为A、B，若
，求
最小时，弦PQ、RS所在直线的方程;
（III）是否存在一定点T，使得
？若存在，求出P的坐标，若不存在，试说明理由.
得分
评卷人
复评人
21．（本小题满分14分）
已知曲线C：
，C上的两点A、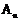
的横坐标分别为2与
，
，数列
满足
（
且
，
）．设区间
，当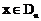
时，曲线C上存在点
，使得点
处的切线与
平行．
（I）建立
与
的关系式；
（II）证明：
是等比数列；
（III）当
对一切
恒成立时，求t的范围．
