1.计算 ,结果是
,结果是
A
8
B ―
2在图(1)的几何体中,它的左视图是
3.下列计算正确的是
A 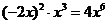 B
B
 C
C  D
D

4. 国家质检总局出台了国内销售的纤维制品甲醛含量标准, 从
A.75×10-7; B.75×10-6; C.7.5×10-6; D.7.5×10-5
 5.从边长为
5.从边长为 的大正方形纸板中挖去一个边长为
的大正方形纸板中挖去一个边长为 的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为
( )
的小正方形纸板后,将其裁成四个相同的等腰梯形(如图甲),然后拼成一个平行四边形(如图乙).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为
( )
A. C.
C.
B. D.
D. 
6.有三十位同学参加智力竞赛,且他们的分数互不相同,取十五位同学进入下一轮比赛,某人知道了自己的分数后,还需知道这十五位同学分数的什么量,就能判断他能不能进入下一轮比赛( )
A、平均数 B、众数 C、最高分数 D、中位数
 7.“五一黄金周”期间,几位同学一起去郊外游玩。男同学都背着红色的旅行包,女同学都背着黄色的旅行包。其中一位男同学说,我看到红色旅行包个数是黄色旅行包个数的1.5倍。另一位女同学却说,我看到的红色旅行包个数是黄色旅行包个数的2倍。如果这两位同学说的都对,那么女同学的人数是( )。
7.“五一黄金周”期间,几位同学一起去郊外游玩。男同学都背着红色的旅行包,女同学都背着黄色的旅行包。其中一位男同学说,我看到红色旅行包个数是黄色旅行包个数的1.5倍。另一位女同学却说,我看到的红色旅行包个数是黄色旅行包个数的2倍。如果这两位同学说的都对,那么女同学的人数是( )。
A.2
B.
8.如图,直线AD与△ABC的外接圆相切于点A,
若∠B=60°,则∠CAD等于
A. 30° B.60° .C 90°D. 120°

 9. 已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2
9. 已知:如图1,点G是BC的中点,点H在AF上,动点P以每秒2 的速度沿图1的边线运动,运动路径为:GàCàDàEàFàH,相应的△ABP的面积
的速度沿图1的边线运动,运动路径为:GàCàDàEàFàH,相应的△ABP的面积 关于运动时间
关于运动时间 的函数图像如图2,若
的函数图像如图2,若 ,则下列四个结论中正确的个数有( )
,则下列四个结论中正确的个数有( )
①图1中的BC长是8 ②图2中的M点表示第4秒时
②图2中的M点表示第4秒时 的值为24
的值为24
③图1中的CD长是4 ④图2中的N点表示第12秒时
④图2中的N点表示第12秒时 的值为18
的值为18
A.1个 B.2个 C.3个 D.4个
10.如图所示:边长分别为 和
和 的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为
的两个正方形,其一边在同一水平线上,小正方形沿该水平线自左向右匀速穿过大正方形,设穿过的时间为 ,大正方形内除去小正方形部分的面积为
,大正方形内除去小正方形部分的面积为 (阴影部分),那么
(阴影部分),那么 与
与 的大致图象应为( )
的大致图象应为( )
 |
总分
核分人
2008年河北省课程改革实验区初中毕业生学业模拟考试
卷II(非选择题,共100分)
注意事项:1.答卷II前,将密封线左侧的项目填写清楚.
2.答卷II时,将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上.
题号
二
三
19
20
21
22
23
24
25
26
得分
得 分
评卷人
题中横线上)
11.分解因式 =_________________.
=_________________.
12.母线长为
13.在课题学习时,老师布置画一个三角形ABC,使∠A=30°,AB=
 14.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,根据图中的信息,估计小张和小李两人中新手是 。
14.小张和小李去练习射击,第一轮10枪打完后两人的成绩如图所示,通常新手的成绩不太稳定,根据图中的信息,估计小张和小李两人中新手是 。
 15.如图,矩形
15.如图,矩形 中,
中, ,将矩形
,将矩形 在直线
在直线 上按顺时针方向不滑动的每秒转动
上按顺时针方向不滑动的每秒转动 ,转动3秒后停止,则顶点
,转动3秒后停止,则顶点 经过的路线长为
.
经过的路线长为
.
16.观察分析下列数据,寻找规律: 0, ,
, ,
,
3,2 ,
, ,3
,3 ,……那么第10个数据应
,……那么第10个数据应
 是
.
是
.
17.如图, 是反比例函数
是反比例函数 在第一象限内的图象,且过点
在第一象限内的图象,且过点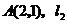 与
与 关于
关于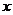 轴对称,那么图象
轴对称,那么图象 的函数解析式为
(
的函数解析式为
( ).
).
18.已知矩形A的边长分别为a和b,如果总有另一矩形B,使得矩形B与矩形A的周长之比与面积之比都等于k,则k的最小值为 .
得 分
评卷人
19.(本小题满分7分)
 解下列不等式组,并在数轴上表示出该不等式组的解集。
解下列不等式组,并在数轴上表示出该不等式组的解集。
 |
得 分
评卷人
20.(本小题满分7分)
如图,已知:CD为一幢
(1)按比例较精确地作出高楼AB及它的最大影长AE;
(2)问若大楼AB建成后是否影响温室CD的采光,试说明理由。
 |
得 分
评卷人
21.(本小题满分10分)
小明和哥哥得到了一张音乐演唱会的门票,两人都很想前往,可票只有一张.哥哥想了一个办法:拿8张扑克牌,将数字为3、4、7、9的四张给小明,将数字为2、5、6、8的四张留给自己,并按如下游戏方式进行确定:小明和哥哥从四张扑克牌中随机抽出一张,将抽出得到的两张扑克牌数字相加,如果和为偶数,则小明获胜,该小明去;如果和为奇数,则哥哥获胜,该哥哥去.
(1)你认为该游戏规则是否公平?请画树状图或列表予以说明;
(2)如果该游戏规则不公平,请你改变一下游戏方案,使得游戏规则公平;如果该游戏规则公平,请你制订一个不公平的游戏规则.




得 分
评卷人
22.(本小题满分8分)
如图1,在桌面内,直线l上摆放着两块大小相同的直角三角板,它们中较小直角边的长为
(1)
将△ECD沿直线AC翻折到如图1(a)的位置, 与AB相交于点F,
与AB相交于点F,
证明: ;
;

(2)将△ECD沿直线l向左平移到1(b)的位置,使E点落在AB上,请你求出平移的距离;
 |

(3)将△ECD绕点C逆时针方向旋转到图1(c)的位置,使E点落在AB上,请你求出旋转角的度数.
 |
得 分
评卷人
23.(本小题满分10分)
蔬菜基地种植某种蔬菜,由市场行情分析知,1月份至6月份这种蔬菜的上市时间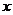 (月份)与市场售价
(月份)与市场售价 (元/千克)的关系如下表:
(元/千克)的关系如下表:
上市时间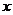 (月份)
(月份)
1
2
3
4
5
6
市场售价 (元/千克)
(元/千克)
10.5
9
7.5
6
4.5
3
这种蔬菜每千克的种植成本 (元/千克)与上市时间
(元/千克)与上市时间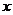 (月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(月份)满足一个函数关系,这个函数的图象是抛物线的一段(如图).
(1)写出上表中表示的市场售价 (元/千克)关于上市时间
(元/千克)关于上市时间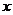 (月份)的函数关系式;
(月份)的函数关系式;
(2)若图中抛物线过 点,写出抛物线对应的函数关系式;
点,写出抛物线对应的函数关系式;
 (3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
(3)由以上信息分析,哪个月上市出售这种蔬菜每千克的收益最大?最大值为多少?(收益=市场售价-种植成本)
得 分
评卷人
24.(本小题满分10分)
在正方形 中,点
中,点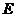 是
是 上一动点,
上一动点, 分别交
分别交 于
于 ,连结
,连结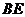 交
交 于点
于点 ,过
,过 作
作 分别交
分别交 于
于 .
.
探究:(1)如图①,当点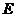 在边
在边 上时,请你动手测量三条线段
上时,请你动手测量三条线段 的长度,猜测
的长度,猜测 与
与 之间的数量关系,并证明你所猜测的结论;
之间的数量关系,并证明你所猜测的结论;
探究:(2)如图②,若点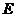 在
在 的延长线上时,
的延长线上时, 之间的数量关系又是怎样?请直接写出结论;
之间的数量关系又是怎样?请直接写出结论;
再探究:(3)如图③,连结并延长 交
交 的延长线
的延长线 于
于 ,若点
,若点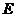 分别在线段
分别在线段 和射线
和射线 上时,请在图③中完成符合题意的图形,并判断
上时,请在图③中完成符合题意的图形,并判断 之间的数量关系又分别怎样?请直接写出结论.
之间的数量关系又分别怎样?请直接写出结论.
 |
得 分
评卷人
25.(本小题满分12分)
某电器经营业主计划购进一批同种型号的挂式空调和电风扇,若购进8台空调和20台电风扇,需要资金17400元,若购进10台空调和30台电风扇,需要资金22500元.
(1)求挂式空调和电风扇每台的采购价各是多少元?
(2)该经营业主计划购进这两种电器共70台,而可用于购买这两种电器的资金不超过30000元,根据市场行情,销售一台这样的空调可获利200元,销售一台这样的电风扇可获利30元.该业主希望当这两种电器销售完时,所获得的利润不少于3500元.试问该经营业主有哪几种进货方案?哪种方案获利最大?最大利润是多少?
得 分
评卷人
26.如图,平面直角坐标系中,四边形 为矩形,点
为矩形,点 的坐标分别为
的坐标分别为 ,动点
,动点 分别从
分别从 同时出发.以每秒1个单位的速度运动.其中,点
同时出发.以每秒1个单位的速度运动.其中,点 沿
沿 向终点
向终点 运动,点
运动,点 沿
沿 向终点
向终点 运动.过点
运动.过点 作
作 ,交
,交 于
于 ,连结
,连结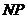 ,已知动点运动了
,已知动点运动了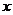 秒.
秒.
(1)用含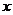 的代数式表示
的代数式表示 点的坐标为;
点的坐标为;
(2)试求 面积
面积 的表达式,并求出面积
的表达式,并求出面积 的最大值及相应的
的最大值及相应的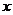 值;
值;
(3)当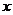 为何值时,
为何值时, 是一个等腰三角形?简要说明理由.
是一个等腰三角形?简要说明理由.
 |
2008年初中毕业生学业考试



















