A. 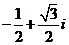 B.
B. 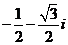 C.
C.
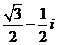 D.
D.
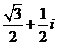
A. 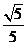 B.
B.
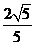 C.
C.
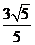 D.
D.
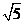
A. 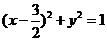 B.
B. 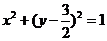 C.
C.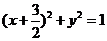 D.
D. 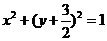
A. 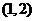 B.
B.
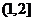 C.
C.
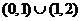 D.
D.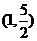

7.从装有2个红球和2个白球的口袋内任取2个球,下列两个事件关系为互斥而不对立的是
A.至少有1个白球;都是白球 B.至少有1个白球;至少有1个白球
C.恰有1个白球;恰有2个白球 D.至少有1个白球;都是红球
8.用1,2,3这三个数字组成四位数,规定这三个数字必须都使用,但相同的数字不能相邻,以这样的方式组成的四位数共有
A.9个 B.18个 C.12个 D. 36个
A. 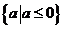 B.
B.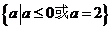
 C.
C.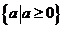
 D.
D. 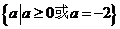

16. (本小题满分12分)
已知函数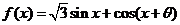 的定义域为R,最大值为1(其中
的定义域为R,最大值为1(其中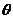 为常数,且
为常数,且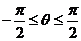 )。
)。
(1) 求角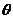 的值;
的值;
(2) 若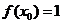 ,求
,求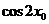 的值。
的值。
17.(本小题满分12分)
 如图,在斜三棱柱
如图,在斜三棱柱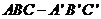 中,
中,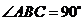 ,则侧面
,则侧面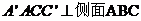 ,又
,又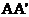 和底面所成
和底面所成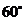 的角,且
的角,且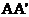 =2a,AB=BC=
=2a,AB=BC=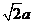 .
.
(1)求平面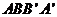 与底面ABC所成的角的正切值;
与底面ABC所成的角的正切值;
(2)求侧面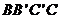 的面积。
的面积。
18.(本小题满分12分)
假设设备的使用年限x与维修费用y(万元)有如下关系:
使用年限x(年)
2
3
4
5
6
维修费用y(万元)
2.2
3.8
5.5
6.5
7.0
(1) 如果y与x之间具有线性相关关系,求回归直线方程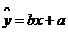 ;
;
(2) 估计使用年限为10年时维修费用是多少?
参考公式: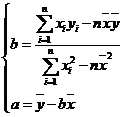
19.(本小题满分12分)
(1)已知函数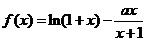 (其中a为常数),求函数f(x)的单调区间;
(其中a为常数),求函数f(x)的单调区间;
(2)求证:不等式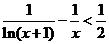 在
在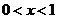 上恒成立。
上恒成立。
20.(本小题满分13分)
如图,在椭圆C: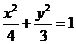 中,
中,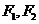 分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,
分别为椭圆C的左右两个焦点,P为椭圆上且在第一象限内的点,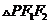 的重心为G,内心为I。
的重心为G,内心为I。
(1) 求证:IG//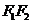 ;
;
(2) 已知A为椭圆C的左顶点,直线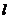 过右焦点
过右焦点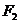 与椭圆C交于M,N两点,若AM,AN的斜率
与椭圆C交于M,N两点,若AM,AN的斜率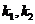 满足
满足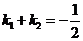 ,求直线
,求直线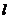 的方程。
的方程。
21.(本小题满分14分)
已知数列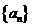 满足递推关系式:
满足递推关系式: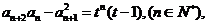 且
且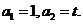 (t为常数,
(t为常数,
且t〉1)
(1) 求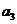
(2) 求证: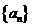 满足关系式
满足关系式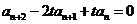 ,(
,(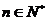 );
);
(3) 求证: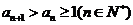

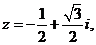 则
则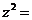
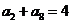 ,则其前9项的和
,则其前9项的和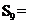
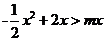 的解集为
的解集为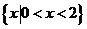 ,则实数m的值为
,则实数m的值为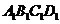 中,M为
中,M为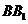 的中点,则点D到直线
的中点,则点D到直线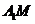 的距离为
的距离为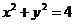 上一点R,动点满足
上一点R,动点满足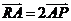 ,则点P的轨迹方程为
,则点P的轨迹方程为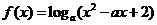 在区间
在区间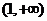 上恒为正值,则实数a的取值范围为
上恒为正值,则实数a的取值范围为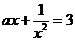 有且仅有一个正实数解,那么实数a的取值范围为
有且仅有一个正实数解,那么实数a的取值范围为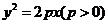 于P,Q两点,若
于P,Q两点,若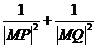 为定值,则a=
为定值,则a=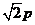 B.
B.
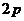 C.
C.
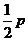 D.
D.
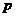
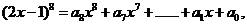 则
则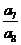 =____________________
=____________________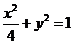 和双曲线
和双曲线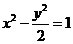 的一个交点,
的一个交点,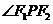 的余弦值为__________________
的余弦值为__________________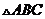 的两条中线的长度分别为6,3,则
的两条中线的长度分别为6,3,则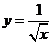 的切线
的切线