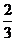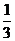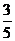1.已知函数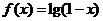 的定义域为集合A,函数
的定义域为集合A,函数 的定义域为集合B,则
的定义域为集合B,则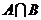 等于
等于
(A)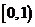 (B)
(B)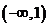 (C)
(C)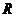 (D)
(D)
2.已知 是第三象限的角,并且sin
是第三象限的角,并且sin =
=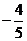 ,则
,则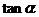 等于
等于
(A) (B)
(B) (C)
(C) (D)
(D)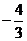
3.在复平面内,与复数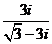 对应的点位于
对应的点位于
(A)第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限
4.如果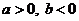 ,那么下列不等式中正确的是
,那么下列不等式中正确的是
(A) (B)
(B) (C)
(C) (D)
(D)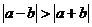
5.设向量 ,则“
,则“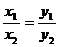 ”是“
”是“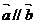 ”的
”的
(A)充要条件 (B)必要不充分条件
(C)充分不必要条件 (D)既不充分也不必要条件
6.过坐标原点且与圆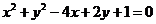 相切的直线方程为
相切的直线方程为
(A) (B)
(B)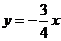 (C)
(C) 或
或 (D)
(D)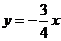 或
或
7.正三角形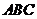 的三个顶点在球
的三个顶点在球 的表面上,
的表面上, ,球心
,球心 到平面
到平面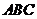 的距离为1,则球
的距离为1,则球 的表面积为
的表面积为
(A) (B)
(B)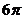 (C)
(C)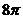 (D)
(D)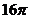
8.在等差数列 和等比数列
和等比数列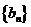 中,
中,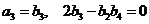 ,则数列
,则数列 前5项的和
前5项的和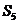 为
为
(A)5 (B)10 (C)20 (D)40
9.已知函数 的图象为
的图象为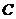 ,则下列命题中
,则下列命题中
①函数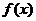 的周期为
的周期为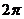 ;
②函数
;
②函数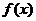 在区间
在区间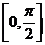 的最小值为
的最小值为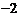 ;
;
③图象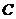 关于直线
关于直线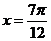 对称; ④图象
对称; ④图象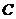 关于点
关于点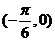 对称.
对称.
正确的命题个数为
(A)1 (B)2 (C)3 (D)4
10.某学校在一次数学基础测试统计中, 所有学生成绩服从正态分布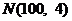 (单位:分),现任选一名学生, 该生成绩在
(单位:分),现任选一名学生, 该生成绩在 分~104分内的概率是
分~104分内的概率是
(A)
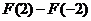 (B)
(B)  (C)
(C) (D)
(D)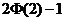
11.我省某电力部门有5名电力技术员 、
、 、
、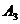 、
、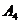 、
、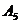 和4名电力工程师
和4名电力工程师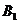 、
、 、
、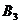 、
、 ,现从中选派2名技术员和1名工程师支援某省今年年初遭受的严重雪灾灾后电力修复工作, 如果
,现从中选派2名技术员和1名工程师支援某省今年年初遭受的严重雪灾灾后电力修复工作, 如果 、
、 两名技术员只能同时选派或同时不选派,技术员
两名技术员只能同时选派或同时不选派,技术员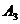 和工程师
和工程师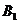 不能同时选派,则不同的选派方案有
不能同时选派,则不同的选派方案有
(A)16种 (B)15种 (C) 14种 (D) 13种
 12.路灯距地面
12.路灯距地面 , 一身高
, 一身高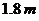 的人沿穿过灯下的直路以
的人沿穿过灯下的直路以 的速度自O处按图示方向行走, 则人影长度变化速率是
的速度自O处按图示方向行走, 则人影长度变化速率是
(A)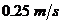 (B)
(B)
(C)
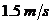 (D)
(D)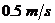
机密★启用前 【考试时间:5月8日 15:00~17:00】
昆明市2008届高三适应性考试
理科数学试卷
第Ⅱ卷(非选择题,共90分)
注意事项:第Ⅱ卷 共2页,共10小题 ,请用黑色碳素笔将答案答在答题卡上,答在试卷上的答案无效.
13.函数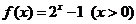 的反函数为
的反函数为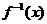 ,则
,则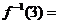 .
.
14.已知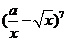 的展开式中
的展开式中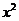 项的系数为3,则实数
项的系数为3,则实数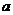 的值为 .(用数字作答)
的值为 .(用数字作答)
15.已知双曲线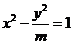 与椭圆
与椭圆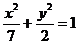 有相同的焦点,则双曲线的渐近线方程为
.
有相同的焦点,则双曲线的渐近线方程为
.
16.棱长为1的正方体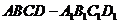 中,点
中,点 、
、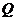 、
、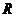 分别是表面
分别是表面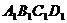 、
、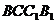 、
、
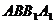 的中心,给出下列结论:
的中心,给出下列结论:
①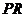 与
与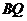 是异面直线;
是异面直线;
②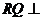 平面
平面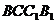 ;
;
③平面 ∥平面
∥平面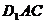 ;
;
④过 、
、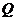 、
、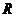 的平面截该正方体所得截面是边长为
的平面截该正方体所得截面是边长为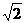 的等边三角形.
的等边三角形.
以上结论正确的是 .(写出所有正确结论的序号)
17.(本小题满分10分)
在△ABC中,a、b、c分别为角A、B、C的对边,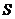 表示该三角形的面积,且
表示该三角形的面积,且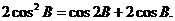
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若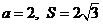 ,求b的值.
,求b的值.
18.(本小题满分12分)
在2008年北京奥运会某项目的选拔比赛中,  、
、 两个代表队进行对抗赛, 每队三名队员,
两个代表队进行对抗赛, 每队三名队员,  队队员是
队队员是
 队队员是
队队员是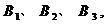 按以往多次比赛的统计, 对阵队员之间胜负概率如下表, 现按表中对阵方式出场进行三场比赛, 每场胜队得1分, 负队得0分, 设A队、B队最后所得总分分别为
按以往多次比赛的统计, 对阵队员之间胜负概率如下表, 现按表中对阵方式出场进行三场比赛, 每场胜队得1分, 负队得0分, 设A队、B队最后所得总分分别为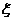 、
、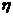 , 且
, 且 .
.
(Ⅰ)求A队得分为2分的概率;
(Ⅱ)求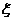 的分布列;并用统计学的知识说明哪个队实力较强.
的分布列;并用统计学的知识说明哪个队实力较强.
对阵队员
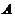 队队员胜
队队员胜
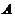 队队员负
队队员负
 对
对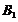
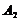 对
对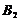
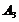 对
对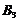
19.(本小题满分12分)
如图,直三棱柱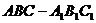 ,
,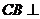 平面
平面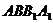 ,
,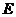 是棱
是棱 上一点,
上一点, 是
是 的中点,
的中点,
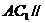 平面
平面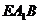 ,
,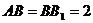 ,二面角
,二面角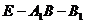 的大小为
的大小为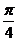 .
.
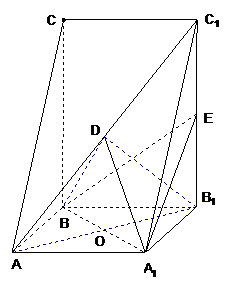 (Ⅰ)求
(Ⅰ)求 的长;
的长;
(Ⅱ)求二面角 的大小.
的大小.
20.(本小题满分12分)
设函数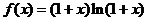 .
.
(Ⅰ)求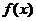 的单调区间;
的单调区间;
(Ⅱ)若 ,且对任意
,且对任意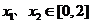 总有
总有 成立,求实数
成立,求实数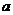 的取值范围.
的取值范围.
21.(本小题满分12分)
设点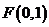 ,动圆
,动圆 经过点
经过点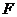 且和直线
且和直线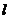 :
: 相切. 记动圆的圆心
相切. 记动圆的圆心 的轨迹为曲线
的轨迹为曲线 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)设点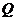 为直线
为直线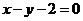 上的动点,过点
上的动点,过点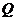 作曲线
作曲线 的切线
的切线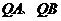 (
(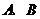 为切点),
为切点),
证明:直线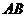 必过定点并指出定点坐标.
必过定点并指出定点坐标.
22.(本小题满分12分)
在数列 中,已知
中,已知 ,
, 
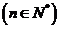
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若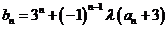 (
(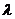 为非零常数),问是否存在整数
为非零常数),问是否存在整数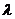 ,使得对任意
,使得对任意 都有
都有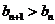 ?若存在,求出
?若存在,求出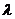 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
昆明市2008届高三适应性考试