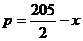(1)与命题“若 ,则
,则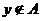 ”等价的命题是
”等价的命题是
(A)若 ,则
,则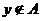 (B)若
(B)若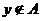 ,则
,则
(C)若 ,则
,则 (D)若
(D)若 ,则
,则
(2)已知三角形的边长分别为 、
、 、
、 ,则它的最大内角的度数是
,则它的最大内角的度数是
(A)90° (B)120° (C)135° (D)150°
(3)已知 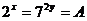 ,且
,且 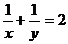 ,则
,则  的值是
的值是
(A)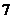 (B)
(B) (C)
(C) (D)
(D)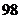
(4)设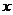 、
、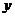 都是正数,则
都是正数,则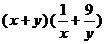 的最小值是
的最小值是
(A)6 (B)16 (C)26 (D)36
(5)已知函数  ,则
,则 
(A)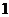 (B)
(B)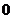 (C)
(C) (D)
(D)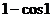
(6)已知有
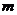 、
、 为两条不同的直线,
为两条不同的直线,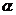 、
、 为两个不同的平面,则下列命题中正确的命题是
为两个不同的平面,则下列命题中正确的命题是
(A)若  ,
,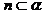 ,
,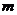 ∥
∥ ,
, ∥
∥ ,则
,则 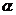 ∥
∥
(B)若  ,
, ,
,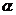 ∥
∥ ,则
,则 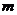 ∥
∥
(C)若  ,
, ,则
,则  ∥
∥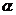
(D)若 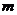 ∥
∥ ,
, ,则
,则 
(7)已知 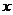 ,
,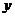 满足约束条件
满足约束条件  则
则 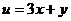 的最大值是
的最大值是
(A)12 (B)15 (C)17 (D)20
(8)已知等比数列的各项均为正数,其前 项和为
项和为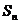 ,且
,且 ,
, ,则此等比数列的公比等于
,则此等比数列的公比等于
(A) (B)
(B)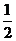 (C)
(C) (D)
(D)
(9)已知双曲线的中心在坐标原点,焦点在 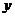 轴上,一条渐近线的方程为
轴上,一条渐近线的方程为  ,则它的离心率为
,则它的离心率为
(A)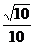 (B)
(B)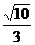 (C)
(C)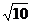 (D)
(D)
(10)右图是计算 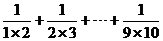 的
的
值的算法框图,其中在判断框中应填入的
条件是
(A)
(B)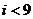
(C)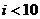
(D)
(11)一个袋子里装有编号为1,2,…,12的12个相同大小的小球,其中1到6号球是红色球,其余为黑色球.若从中任意摸出一个球,记录它的颜色和号码后再放回到袋子里,然后再摸出一个球,记录它的颜色和号码,则两次摸出的球都是红球,且至少有一个球的号码是偶数的概率是
(A)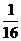 (B)
(B)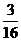 (C)
(C) (D)
(D)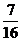
(12)定义域为
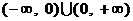 的函数
的函数 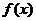 不恒为零,且对于定义域内的任意实
不恒为零,且对于定义域内的任意实
数 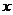 、
、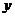 都有
都有  成立,则
成立,则 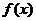
(A)是奇函数,但不是偶函数 (B)是偶函数,但不是奇函数
(C)既是奇函数,又是偶函数 (D)既不是奇函数,又不是偶函数
第Ⅱ卷(非选择题 共90分)
注意事项:
1. 请用
2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效.
3. 第Ⅱ卷共包括填空题和解答题两道大题.
(13)某地球仪上北纬30°纬线的长度为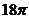 cm,则该地球仪的表面积是 cm2 .
cm,则该地球仪的表面积是 cm2 .
(14)已知复数 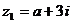 (
( 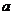 为实数,
为实数,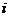 为虚数单位),
为虚数单位),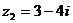 ,且
,且 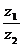 为纯虚数,
为纯虚数,
则实数 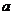 的值是
.
的值是
.
(15)过点(0,―1)的直线与抛物线  相交于 A、B 两点,O 为坐标原点,则
相交于 A、B 两点,O 为坐标原点,则
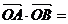 .
.
(16)已知在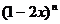 的展开式中,各项的二项式系数之和是64,则
的展开式中,各项的二项式系数之和是64,则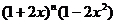 的展开式中,
的展开式中,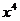 项的系数是 .
项的系数是 .
(17)(本小题满分12分)
向量m  (
(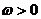 ),n
),n 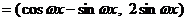 ,函数
,函数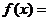 m
m n
n ,若
,若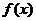 图象上相邻两个对称轴间的距离为
图象上相邻两个对称轴间的距离为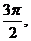 且当
且当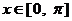 时,函数
时,函数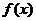 的最小值为0.
的最小值为0.
(Ⅰ)求函数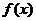 的表达式;
的表达式;
(Ⅱ)在△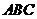 中, 若
中, 若 ,且
,且  ,求
,求  的值.
的值.
(18)(本小题满分12分)
 如图所示,已知四棱锥 S―ABCD
的底面 ABCD 是矩形,M、N 分别是 CD、SC 的中点,SA ⊥底面ABCD,SA = AD = 1,AB =
如图所示,已知四棱锥 S―ABCD
的底面 ABCD 是矩形,M、N 分别是 CD、SC 的中点,SA ⊥底面ABCD,SA = AD = 1,AB =  .
.
(Ⅰ)求证:MN ⊥平面ABN;
(Ⅱ)求二面角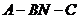 的余弦值.
的余弦值.
(19)(本小题满分12分)
某企业准备投产一种新产品,经测算,已知每年生产
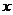 (
(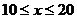 )万件的该种
)万件的该种
产品所需要的总成本为 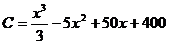 (
(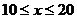 )万元,市场销售情况
)万元,市场销售情况
可能出现好、中、差三种情况,各种情况发生的概率和相应的价格 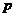 (元)与年产量
(元)与年产量 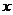 之间的函数关系如下表所示.
之间的函数关系如下表所示.
市场情况
概率
价格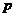 与产量
与产量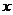 的函数关系式
的函数关系式
好
0.3
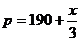
中
0.5

差
0.2
设 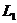 、
、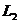 、
、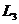 分别表示市场情况好、中、差时的利润,随机变量
分别表示市场情况好、中、差时的利润,随机变量
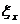 表示当年产量为
表示当年产量为 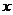 而市场情况不确定时的利润.
而市场情况不确定时的利润.
(Ⅰ)分别求利润 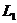 、
、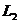 、
、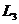 与年产量
与年产量 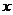 之间的函数关系式;
之间的函数关系式;
(Ⅱ)当产量 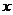 确定时,求随机变量
确定时,求随机变量 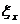 的期望
的期望 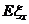 ;
;
(Ⅲ)求年产量 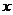 为何值时,随机变量
为何值时,随机变量 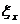 的期望
的期望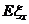 取得最大值(不需求最大值).
取得最大值(不需求最大值).
(20)(本小题满分12分)
已知函数 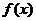 与
与 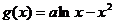 (
(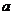 为常数)的图象关于直线
为常数)的图象关于直线 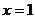 对称,且
对称,且 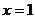 是
是 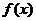 的一个极值点.
的一个极值点.
(Ⅰ)求出函数 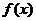 的表达式和单调区间;
的表达式和单调区间;
(Ⅱ)若已知当 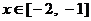 时,不等式
时,不等式 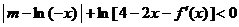 恒成立,求
恒成立,求 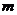 的取值范围.
的取值范围.
(21)(本小题满分12分)
已知椭圆C: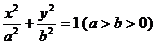 的中心关于直线
的中心关于直线 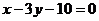 的对称点落在直线
的对称点落在直线 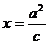 (其中
(其中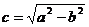 )上,且椭圆 C 的离心率为
)上,且椭圆 C 的离心率为 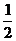 .
.
(Ⅰ)求椭圆 C 的方程;
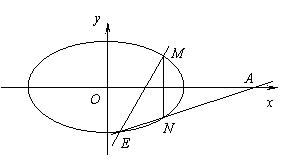
(Ⅱ)设A(3,0),M、N 是椭圆 C 上关于 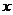 轴对称的任意两点,连结 AN 交椭圆于另一点 E,求证直线 ME 与
轴对称的任意两点,连结 AN 交椭圆于另一点 E,求证直线 ME 与 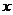 轴相交于定点.
轴相交于定点.
 |
(22)(本小题满分14分)
数列  满足:
满足: (
( ),且
),且  (
( ,
,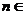 N?).
N?).
(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
2008年威海市高考模拟考试