(1)与命题“若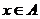 ,则
,则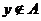 ”等价的命题是
”等价的命题是
(A)若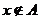 ,则
,则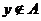 (B)若
(B)若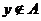 ,则
,则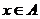
(C)若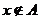 ,则
,则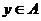 (D)若
(D)若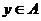 ,则
,则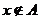
(2)已知三角形的边长分别为 、
、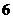 、
、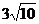 ,则它的最大内角的度数是
,则它的最大内角的度数是
(A)90° (B)120° (C)135° (D)150°
(3)已知 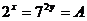 ,且
,且 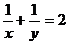 ,则
,则 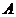 的值是
的值是
(A)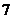 (B)
(B)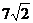 (C)
(C)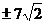 (D)
(D)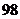
(4)设 、
、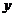 都是正数,则
都是正数,则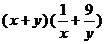 的最小值是
的最小值是
(A)6 (B)16 (C)26 (D)36
(5)过点 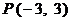 作圆
作圆 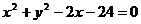 的切线,则切线方程是
的切线,则切线方程是
(A)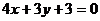 (B)
(B)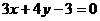
(C)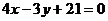 (D)
(D)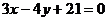
(6)已知有 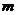 、
、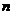 为两条不同的直线,
为两条不同的直线,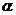 、
、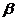 为两个不同的平面,则下列命题中正确的命题是
为两个不同的平面,则下列命题中正确的命题是
(A)若 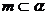 ,
,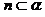 ,
,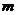 ∥
∥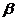 ,
,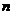 ∥
∥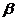 ,则
,则 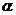 ∥
∥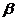
(B)若 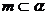 ,
,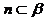 ,
,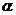 ∥
∥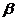 ,则
,则 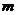 ∥
∥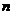
(C)若 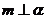 ,
,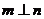 ,则
,则 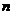 ∥
∥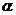
(D)若 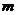 ∥
∥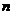 ,
,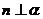 ,则
,则 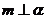
(7)已知  ,
,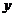 满足约束条件
满足约束条件 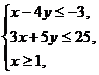 则
则 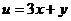 的最大值是
的最大值是
(A)12 (B)15 (C)17 (D)20
(8)已知等比数列的各项均为正数,其前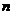 项和为
项和为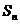 ,且
,且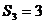 ,
, ,则此等比数列的公比等于
,则此等比数列的公比等于
(A)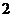 (B)
(B)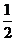 (C)
(C)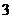 (D)
(D)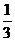
(9)已知双曲线的中心在坐标原点,焦点在 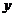 轴上,一条渐近线的方程为
轴上,一条渐近线的方程为 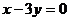 ,则它的离心率为
,则它的离心率为
(A)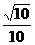 (B)
(B)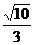 (C)
(C)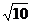 (D)
(D)
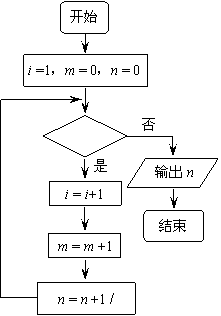
(10)右图是计算 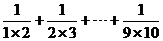 的
的
值的算法框图,其中在判断框中应填入的
条件是
(A)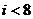
(B)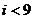
(C)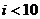
(D)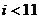
 (11)右图是一个空间几何体的三视图,其主视图和左视图
(11)右图是一个空间几何体的三视图,其主视图和左视图
分别是两个边长为 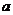 正方形,俯视图是一个直角边长
正方形,俯视图是一个直角边长
为 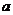 的等腰直角三角形,则这个几何体的体积是
的等腰直角三角形,则这个几何体的体积是
(A)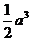 (B)
(B)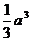
(C)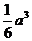 (D)
(D)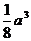
(12)已知
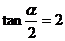 ,则
,则 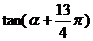 的值是
的值是
(A)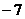 (B)
(B)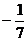 (C)
(C)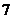 (D)
(D)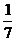
第Ⅱ卷(非选择题 共90分)
注意事项:
1. 请用
2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效.
3. 第Ⅱ卷共包括填空题和解答题两道大题.
(13)某学校有学生2500人,其中高三年级的学生800人,为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校抽取一个200人的样本,则样本中高三学生的人数应为 .
(14)某地球仪上北纬30°纬线的长度为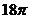 cm,则该地球仪的表面积是 cm2 .
cm,则该地球仪的表面积是 cm2 .
(15)已知复数 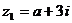 (
( 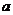 为实数,
为实数,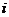 为虚数单位),
为虚数单位),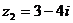 ,且
,且 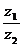 为纯虚数,
为纯虚数,
则实数
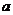 的值是
.
的值是
.
(16)过点(0,―1)的直线与抛物线
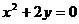 相交于 A、B 两点,O 为坐标原点,则
相交于 A、B 两点,O 为坐标原点,则
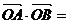 .
.
(17)(本小题满分12分)
将一颗骰子先后抛掷2次,观察向上的点数,求
(Ⅰ)两次向上的点数之和为7或是4的倍数的概率;
(Ⅱ)以第一次向上的点数为横坐标 x,第二次向上的点数为纵坐标 y 的点(x,y)在圆 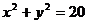 的内部(不包括边界)的概率.
的内部(不包括边界)的概率.
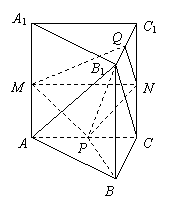 (18)(本小题满分12分)
(18)(本小题满分12分)
如图,在正三棱柱ABC―A1B
分别是AA1、CC1、AC、B
(Ⅰ)求证:MN ⊥ 平面PBB1 ;
(Ⅱ)求证:平面AB
(Ⅲ)若AA1 = 2 AB = 2,求三棱锥 Q ― MNP 的体积.
(19)(本小题满分12分)
向量m 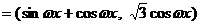 (
(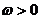 ),n
),n 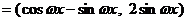 ,函数
,函数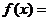 m
m n
n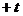 ,若
,若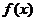 图象上相邻两个对称轴间的距离为
图象上相邻两个对称轴间的距离为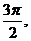 且当
且当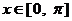 时,函数
时,函数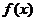 的最小值为0.
的最小值为0.
(Ⅰ)求函数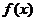 的表达式;
的表达式;
(Ⅱ)在△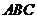 中, 若
中, 若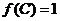 ,且
,且 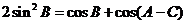 ,求
,求 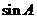 的值.
的值.
(20)(本小题满分12分)
已知函数 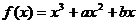 的图象与直线
的图象与直线 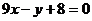 相切于点(
相切于点(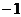 ,
,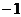 ).
).
(Ⅰ)求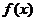 的解析式;
的解析式;
(Ⅱ)求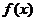 的极值.
的极值.
(21)(本小题满分12分)
已知椭圆C: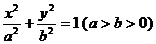 的中心关于直线
的中心关于直线 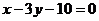 的对称点落在直线
的对称点落在直线 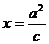 (其中
(其中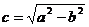 )上,且椭圆 C
的离心率为
)上,且椭圆 C
的离心率为 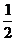 .
.
(Ⅰ)求椭圆 C 的方程;
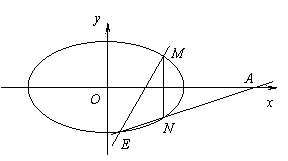
(Ⅱ)设A(3,0),M、N 是椭圆 C
上关于  轴对称的任意两点,连结 AN 交椭圆于另一点 E,求证直线 ME 与
轴对称的任意两点,连结 AN 交椭圆于另一点 E,求证直线 ME 与  轴相交于定点.
轴相交于定点.
 |
(22)(本小题满分14分)
已知数列 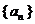 满足:
满足: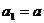 (
(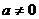 ),且
),且 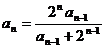 (
(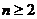 ,
,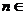 N?).
N?).
(Ⅰ)求证: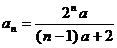 ;
;
(Ⅱ)若 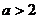 ,求证:
,求证: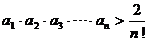 .
.
2008年威海市高考模拟考试