1.设全集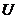 =
= ,
,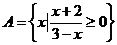 ,
,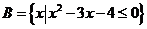 ,则
,则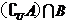 等于
等于
A.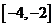 B.
B.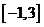 C.
C.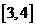 D.
D.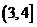
2.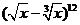 的展开式中,含有
的展开式中,含有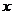 的正整数次幂的项共有
的正整数次幂的项共有
A.4项 B.3项 C.2项 D.1项
3.高三(10)班甲、乙两位同学6次数学测试的成绩如下表:
1
2
3
4
5
6
甲
122
120
125
116
120
117
乙
118
125
120
122
115
120
仅从这6次考试成绩来看,甲、乙两位同学数学成绩稳定的情况是
A.甲稳定 B.乙稳定 C.甲与乙一样稳定 D.不能确定
4.设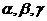 为不同的平面,
为不同的平面,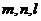 为不同的直线,则
为不同的直线,则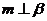 的一个充分不必要条件是
的一个充分不必要条件是
A.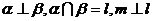 B.
B.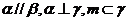
C.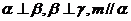 D.
D.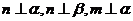
5.在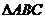 中,已知
中,已知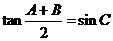 ,则
,则
A. .
B.
.
B.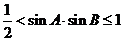 .
.
C.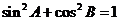 D.
D.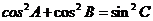
6.已知定义在R上的函数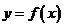 满足下列三个条件:
满足下列三个条件:
①对任意的x∈R都有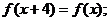
②对于任意的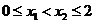 ,都有
,都有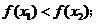
③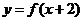 的图象关于y轴对称.
的图象关于y轴对称.
则下列结论中,正确的是
A. 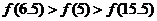 B.
B.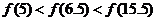
C. 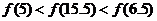 D.
D.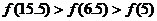
7.A、B、C、D、E五个人住进编号为1,2,3,4,5的五个房间,每个房间只住一人,则B不住2号房间,且B,C两人要住编号相邻房间的住法种数为
A.24
B.
8.椭圆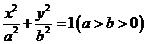 的中心、右焦点、右顶点、右准线与
的中心、右焦点、右顶点、右准线与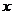 轴的交点依次为O、F、A、H,则
轴的交点依次为O、F、A、H,则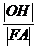 的最小值为
的最小值为
A.2
B.
A.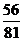 B.
B.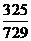 C.
C. 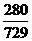 D.
D.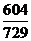
10.设方程 的两根为
的两根为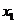 ,
, (
(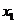 <
< ),则
),则
A.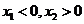 B.
B.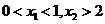 C.
C.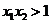 D.
D.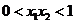
11.在坐标平面上,不等式组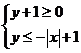 所表示的平面区域的周长为 ▲ .
所表示的平面区域的周长为 ▲ .
12.已知函数 的图象与直线
的图象与直线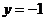 的交点中最近的两点间的距离为
的交点中最近的两点间的距离为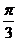 ,则函数
,则函数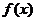 的最小正周期等于 ▲
的最小正周期等于 ▲
13.球O上两点A、B间的球面距离为 ,
,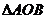 有一个内角为
有一个内角为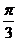 ,则此球的体积是 ▲ .
,则此球的体积是 ▲ .
14.已知双曲线的两条渐近线的夹角为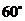 ,则其离心率为
▲ .
,则其离心率为
▲ .
15.若直线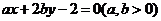 始终平分圆
始终平分圆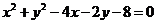 的周长,则
的周长,则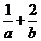 的最小值为
▲
.
的最小值为
▲
.
16.已知函数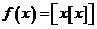 (
(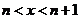 ),其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2.5]=2.定义
),其中[x]表示不超过x的最大整数,如[-2.1]=-3,[-3]=-3,[2.5]=2.定义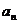 是函数
是函数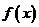 的值域中的元素个数,数列
的值域中的元素个数,数列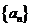 的前n项和为
的前n项和为 ,则满足
,则满足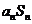
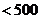 的最大正整数n= ▲
.
的最大正整数n= ▲
.
17.(本题满分12分) 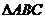 中,角A、B、C所对的边分别为
中,角A、B、C所对的边分别为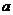 、
、 、
、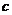 ,已知
,已知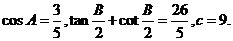
(1)求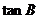 的值;
的值;
(2)求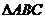 的面积。
的面积。
18. (本题满分14分) 已知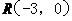 ,点
,点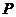 在
在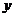 轴上,点
轴上,点 在
在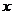 轴的正半轴上,点
轴的正半轴上,点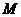 在直线
在直线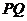 上,且满足
上,且满足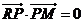 ,
,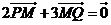 。
。
(1)当点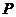 在
在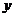 轴上移动时,求
轴上移动时,求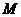 点的轨迹
点的轨迹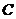 的方程;
的方程;
(2)设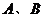 为轨迹
为轨迹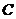 上两点,
上两点,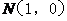 ,
, ,
,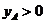 ,若存在实数
,若存在实数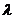 ,使
,使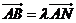 ,且
,且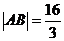 ,求
,求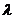 的值。
的值。
 19.(本题满分14分)如图,已知正三棱柱
19.(本题满分14分)如图,已知正三棱柱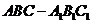 中,
中,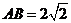 ,
,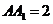 ,三棱锥
,三棱锥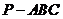 中,
中,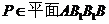 ,且
,且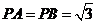 。
。
(1)求证: ;
;
(2)求二面角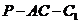 的大小;
的大小;
(3)求点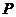 到平面
到平面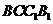 的距离。
的距离。
20.(本题满分14分)设函数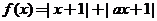 ,已知
,已知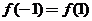 ,且
,且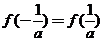 (a∈R,且a≠0),函数
(a∈R,且a≠0),函数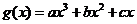 (b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上。
(b∈R,c为正整数)有两个不同的极值点,且该函数图象上取得极值的两点A、B与坐标原点O在同一直线上。
(1)试求a、b的值;
(2)若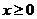 时,函数
时,函数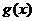 的图象恒在函数
的图象恒在函数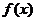 图象的下方,求正整数
图象的下方,求正整数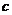 的值。
的值。
21.(本题满分16分)已知数列{an}满足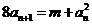 ,
,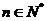 ,
,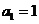 ,
,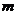 为正数 .
为正数 .
(1)若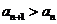 对
对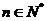 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)是否存在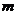 ,使得对任意正整数
,使得对任意正整数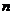 都有
都有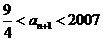 ?若存在,求出
?若存在,求出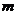 的值;
的值;
若不存在,请说明理由。

