1、若U={1,2,3,4}, M={1,2},N={2,3}, 则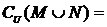 ( )
( )
A.{1,2,3} B. {2} C.{1,3,4} D. {4}
2、已知1是 与
与 的等比中项,又是
的等比中项,又是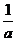 与
与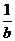 的等差中项,则
的等差中项,则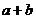 的值为
的值为
A.1 B.2 C.3 D.4
3、将直线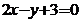 绕着点(-1,1)沿逆时针方向旋转
绕着点(-1,1)沿逆时针方向旋转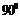 所得的直线方程
所得的直线方程
A. 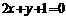 B.
B. 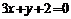 C.
C. 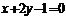 D.
D. 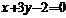
4、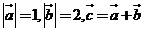 ,且
,且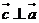 ,则向量
,则向量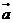 与
与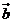 的夹角为
的夹角为
A.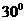 B.
B. 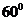 C.
C. 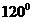 D.
D. 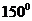
 5、函数y=1-|x-x2|的图象大致是
5、函数y=1-|x-x2|的图象大致是
A. B. C. D.
6、随机变量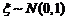 ,记
,记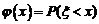 ,则下列式子中错误的是
,则下列式子中错误的是
A.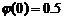 B.
B. 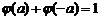
C. 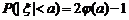 D.
D. 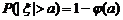
7、设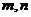 为直线,
为直线,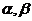 为平面,则
为平面,则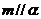 的一个充分不必要条件是
的一个充分不必要条件是
A.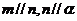 B.
B.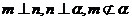 C.
C.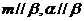 D.
D.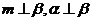 .
.
8、过函数f (x)= x+cosx-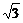 sin x图象上一点的切线的倾斜角是θ,则θ的取值范围是
sin x图象上一点的切线的倾斜角是θ,则θ的取值范围是
A. 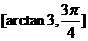 B.
B. 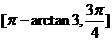
C.  D.
D. 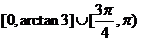
9、在平面直角坐标系中,点 满足
满足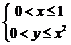 ,点
,点 所在区域的面积为
所在区域的面积为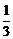 ,
,
则集合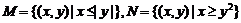 的交集
的交集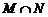 所表示的图形面积为
所表示的图形面积为
A.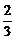 B.
B.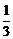 C.1
D.
C.1
D.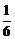
10、一条走廊宽长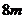 ,
,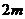 , 用 6 种颜色的
, 用 6 种颜色的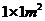 的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有
的整块地砖来铺设(每块地砖都是单色的, 每种颜色的地砖都足够多), 要求相邻的两块地砖颜色不同, 那么所有的不同拼色方法有
A. 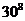 个 B.
个 B. 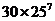 个 C.
个 C. 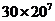 个 D.
个 D. 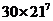 个
个
数学(理科)答卷纸
题号
一
二
三
总分
18
19
20
21
22
得分
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷(非选择题共100分)
11、已知复数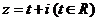 ,且
,且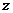 满足
满足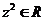 ,则实数
,则实数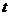 的值为
的值为
12、椭圆的焦距是它的两条准线间距离的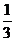 ,则它的离心率为
,则它的离心率为
13、函数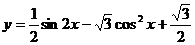 的最小正周期为
的最小正周期为
14、若二项式
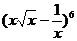 展开式中的第5项是5,则
展开式中的第5项是5,则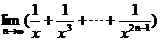 等于
等于
15、棱长为2的正四面体ABCD的外接球的球心O到平面BCD的距离等于
16、已知抛物线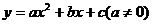 的对称轴在y轴的左侧,其中
的对称轴在y轴的左侧,其中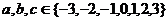 ,在这些抛物线中,记随机变量
,在这些抛物线中,记随机变量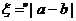 的取值
的取值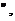
则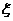 的数学期望
的数学期望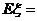
17、定义点 到直线
到直线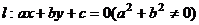 的有向距离为:
的有向距离为:
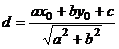 .已知点
.已知点 、
、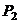 到直线
到直线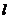 的有向距离分别是
的有向距离分别是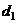 、
、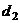 ,有以下命题:
,有以下命题:
①若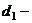
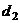 =0,则直线
=0,则直线
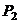 与直线
与直线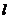 平行;②若
平行;②若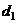 +
+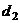 =0,则直线
=0,则直线
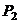 与直线
与直线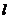 平行;
平行;
③若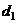 +
+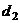 =0,则直线
=0,则直线
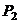 与直线
与直线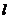 垂直;④若
垂直;④若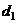
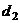 <0,则直线
<0,则直线
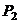 与直线
与直线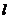 相交。
相交。
以上结论正确的是 .(要求填上正确结论的序号)
18、数列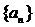 满足:
满足: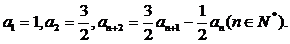
(Ⅰ)记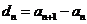 ,求证:
,求证: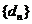 是等比数列;
是等比数列;
(Ⅱ)求数列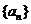 的通项公式;
的通项公式;
19、如图,平面四边形ABCD中, AB=13, AC=10,
AD=5,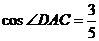 ,
,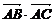 =120,
=120,
(Ⅰ)
求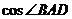 ; (Ⅱ) 设
; (Ⅱ) 设 求实数x、y的值.
求实数x、y的值.
21、已知点D在定线段MN上,且|MN|=3,|DN|=1,一个动圆C过点D且与MN相切,分别过M、N作圆C的另两条切线交于点P.
(Ⅰ)建立适当的平面直角坐标系,求点P的轨迹方程;
 (Ⅱ)过点M作直线l与所求轨迹交于两个不同的点A、B,
(Ⅱ)过点M作直线l与所求轨迹交于两个不同的点A、B,
若 =λ
=λ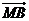 ,且λ∈[2-,2+],记直线l
,且λ∈[2-,2+],记直线l
与直线MN夹角为θ,求 的取值范围.
的取值范围.
22、已知函数 是定义在
是定义在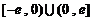 上的奇函数,当
上的奇函数,当 时,有
时,有
(其中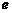 为自然对数的底,
为自然对数的底,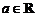 ).
).
(Ⅰ)若 ,求函数
,求函数 的解析式;
的解析式;
(Ⅱ)试问:是否存在实数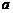 ,使得当
,使得当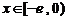 ,
, 的最小值是
的最小值是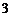 ?如果存在,求出实数
?如果存在,求出实数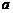 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(Ⅲ)设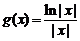 (
(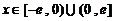 ),求证:当
),求证:当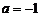 时,
时,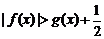 ;
;

 20、如图,正三棱柱ABC―A1B
20、如图,正三棱柱ABC―A1B

