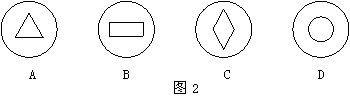
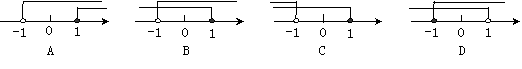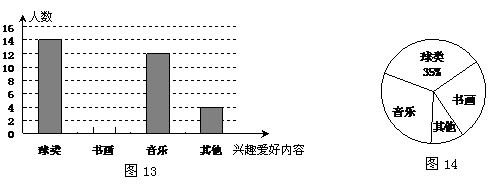1.下列运算结果等于1的是
A.-2+1 B.
2.小明在下面的计算中,有一道题做错了,那么他做错的题目是
A.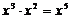 B.
B. 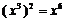 C.
C. 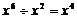 D.
D. 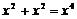
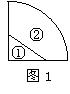
3.将一圆形纸片对折后再对折得图1,然后沿着图中的虚线剪开,得①、②两部分,将②展开后的平面图形可以是图2中的
4.把不等式组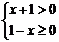 的解集表示在数轴上,正确的是
的解集表示在数轴上,正确的是
5.下列调查,不适合采用抽样方式的是
A.要了解一批灯泡的使用寿命
B.要了解海南电视台“直播海南”栏目的收视率
C.要保证“神舟六号”载人飞船成功发射,对它的重要零部件的检查
D.要了解外地游客对海南旅游服务行业的满意度
6.代数式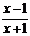 有意义时,
有意义时,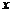 的取值范围是
的取值范围是
A.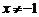 B.
B.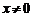 C.
C.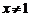 D.
D.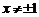
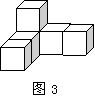
7. 由6个大小相同的正方形搭成的几何体如图3所示,则关于它的视图说法正确的是
A. 正视图的面积最大 B. 左视图的面积最大
C. 俯视图的面积最大 D. 三个视图的面积一样大
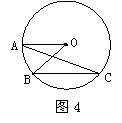
8.如图4,点A、B、C在⊙O上,OA∥BC,∠
A.10° B.25° C.30° D.40°
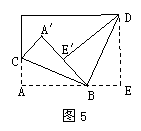
9.将一矩形纸片按图5的方式折叠,BC、BD为折痕,折叠后A/B与E/B在同一条直线上,则下列结论中,不一定正确的是
A. ∠CBD=90° B.DE/⊥A/B C. △A/BC≌△E/DB D. △ABC∽△EDB
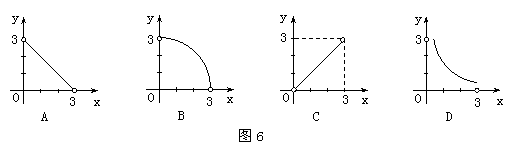 10.
10.  一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形,若小三角形和梯形的面积分别是
一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形,若小三角形和梯形的面积分别是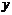 和
和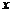 ,则
,则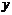 关于
关于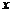 的函数图象大致是图6中的
的函数图象大致是图6中的
 11.计算:
11.计算: 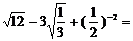 .
.
12.某工厂原计划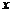 天生产50件产品,若现在需要比
天生产50件产品,若现在需要比
原计划提前1天完成,则现在每天要生产产品 件.
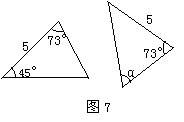
13.如图7,两个三角形全等,其中某些边的长度及某
些角的度数已知,则∠α= 度.
14.在一个不透明的口袋中,装有12个黄球和若干的红球,这些球除颜色外没有其他区别,小李通过很多次摸球试验后发现,从中随机摸出一个红球的频率值稳定在25%,则该袋中有红球的个数很可能是 个.
15.观察下列等式:(1+2)2-4×1=12+4,(2+2)2-4×2=22+4,(3+2)2-4×3=32+4,(4+2)2-4×4=42+4,…,则第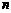 个等式可以是
.
个等式可以是
.
16.如图8,一辆汽车沿着坡度为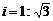 的斜坡向下行驶
的斜坡向下行驶
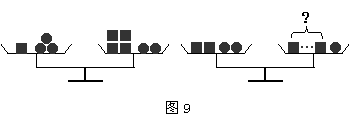 17.如图9的天平中各正方体的质量相同,各小球质量相同,若使两架天平都平衡,则右边天平右端托盘上正方体的个数为
.
17.如图9的天平中各正方体的质量相同,各小球质量相同,若使两架天平都平衡,则右边天平右端托盘上正方体的个数为
.
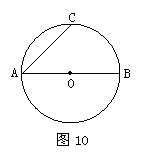
18.如图10,AB为⊙O的直径,其长度为
的中点,若⊙O的另一条弦AD长等于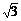 cm,∠CAD的度数为 .
cm,∠CAD的度数为 .
19.(本题满分9分)化简: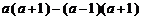 .
.
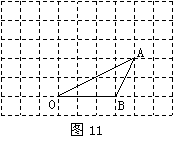 20.(本题满分10分)如图11,点O、B的坐标分别
20.(本题满分10分)如图11,点O、B的坐标分别
为(0,0),(3,0),将△OAB绕点O按逆时针方向旋转90°
到△OA/B/.
(1)画出△OA′B′;
(2)点A′的坐标为 ;
(3)求在旋转过程中,点B所经过的路线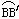 的长度.
的长度.
21.(本题满分10分)在“五一”黄金周期间,小明、小亮等同学随家长一同到热带海洋世界游玩,下面是购买门票时,小明与他爸爸的对话(图12),试根据图中的信息,解答下列问题
 (1)小明他们一共去了几个成人,几个学生?
(1)小明他们一共去了几个成人,几个学生?
(2)请你帮助小明算一算,
用哪种方式购票更省钱?说明理由.
22.(本题满分11分)李华对本班同学的业余兴趣爱好进行了一次调查(每人只统计一项爱好). 他根据采集到的数据,绘制了下面的图13和图14,请你根据图中提供的信息,解答下列问题:
(1)求出李华同学所在班级的总人数及爱好书画的人数;
(2)在图13中画出表示“书画”部分的条形图;
(3)观察图13和图14,请你再写出两条相关结论.
23.(本题满分12分)某公司推出了一种高效环保型除草剂,年初上市后,公司经历了从亏损到盈利的过程.
图15的二次函数图象(部分)刻画了该公司年初以来累积利润S(万元)与时间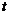 (月)之间的关系(即前
(月)之间的关系(即前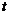 个月的利润总和S与
个月的利润总和S与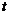 之间的关系).
之间的关系).
根据图象提供信息,解答下列问题:
(1)公司从第几个月末开始扭亏为盈;
(2)求累积利润S与时间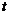 之间的函数关系式;
之间的函数关系式;
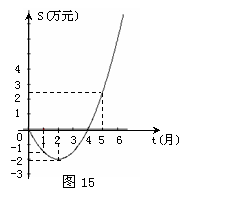 (3)求第8个月公司所获利是多少元?
(3)求第8个月公司所获利是多少元?
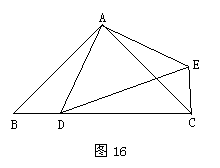
24.(本题满分12分)如图16,D为等腰直角△ABC斜边BC上的一个动点(D与B、C均不重合),连结AD,以AD为直角边作等腰直角△ADE,DE为斜边,连结CE.
(1)求证:△ACE≌△ABD;
(2)设BD=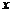 ,若AB=
,若AB=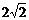
①当△DCE的面积为1.5时,求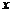 的值;
的值;
②试问:△DCE的面积是否存在最在值,若存在,请求出这个最大值,并指出此时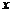 的取值,若不存在,请说明理由.
的取值,若不存在,请说明理由.