1、复数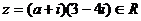 ,则实数a的值是( )
,则实数a的值是( )
A.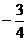 B.
B.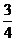 C.
C.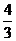 D.-
D.-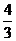
2、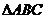 中,若
中,若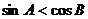 ,则
,则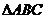 为
( )
为
( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
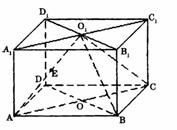
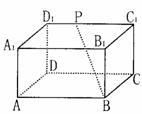 3、如右图,长方体ABCD―A1B
3、如右图,长方体ABCD―A1B
A.是45° B.是60°
C.是90° D.随P点的移动而变化
4、设函数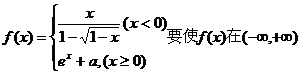 内连续,则实数a值等于( )
内连续,则实数a值等于( )
A.1 B.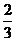 C.
C.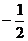 D.
D.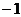
5、关于函数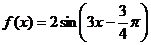 ,有下列命题
,有下列命题
① 其最小正周期为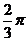 ; ② 其图像由
; ② 其图像由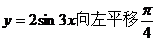 个单位而得到;
个单位而得到;
③ 其表达式写成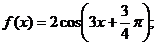 ④ 在
④ 在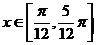 为单调递增函数;
为单调递增函数;
则其中假命题为( )
A.① B.② C.③ D.④
6、已知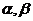 表示平面,m,n表示直线,则m//
表示平面,m,n表示直线,则m//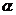 的一个充分而不必要条件是( )
的一个充分而不必要条件是( )
A.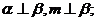 B.
B.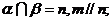 C.
C.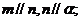 D.
D.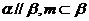
7、若函数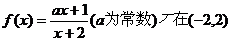 内为增函数,则实数a的取值范围( )
内为增函数,则实数a的取值范围( )
A.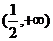 B.
B.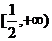 C.
C.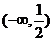 D.
D.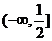
8、已知双曲线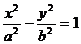 的左焦点为F1,左、右顶点为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A
的左焦点为F1,左、右顶点为A1、A2,P为双曲线上任意一点,则分别以线段PF1,A
A.相交 B.相切 C.相离 D.以上情况都有可能
 9、如图,平面内的两条相交直线
9、如图,平面内的两条相交直线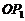 和
和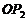 将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若
将该平面分割成四个部分Ⅰ、Ⅱ、Ⅲ、Ⅳ (不包括边界). 若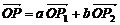 ,且点
,且点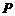 落在第Ⅲ部分,则实数
落在第Ⅲ部分,则实数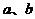 满足( )
满足( )
(A) 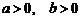 .
(B)
.
(B) 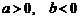 .
.
(C) 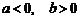 .
(D)
.
(D) 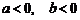 .
.
10、在一次教师联欢会上,到会的女教师比男教师多12人,从这些教师中随机挑选一人表演节目. 若选到男教师的概率为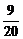 ,则参加联欢会的教师共有( )
,则参加联欢会的教师共有( )
A.120人. B.144人 C.240人 D.360人
11、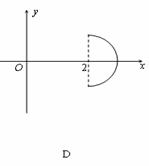
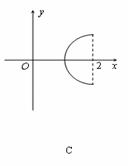 在平面直角坐标系中,已知曲线C:
在平面直角坐标系中,已知曲线C: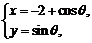 (θ是参数,且
(θ是参数,且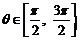 ),那么曲线C关于直线y=x对称的曲线是 ( )
),那么曲线C关于直线y=x对称的曲线是 ( )
12、若不等式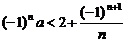 对于任意正整数n恒成立,则实数a的取值范围是( )
对于任意正整数n恒成立,则实数a的取值范围是( )
A.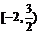 B.
B.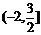 C.
C.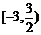 D.
D.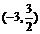
13、已知数列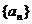 满足
满足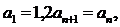 记
记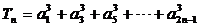 ,
,
则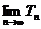 = .
= .
14、已知函数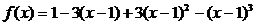 ,则
,则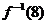 =
.
=
.
15、已知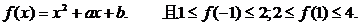 则点
则点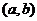 所在区域面积是
所在区域面积是
16、点P(3,1)在椭圆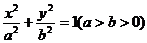
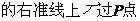
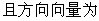 的
的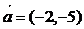 光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
17、(本小题12分) 已知函数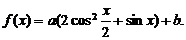
(1)当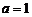 时,求
时,求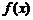 的单调递增区间;
的单调递增区间;
(2)当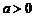 ,且
,且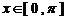 时,
时,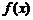 的值域是
的值域是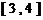 ,求a、b的值.
,求a、b的值.
18、(本小题12分)
旅游公司为3个旅游团提供4条旅游线路,每个旅游团任选其中一条.
(1)求3个旅游团选择3条不同的线路的概率
(2)求恰有2条线路没有被选择的概率.
(3)求选择甲线路旅游团数的期望.
19、(本小题12分) 如图,直四棱柱ABCD―A1B
(1)求二面角O1-BC-D的大小;
(2)求点E到平面O1BC的距离
20、(本小题12分)
在平面直角坐标系中,已知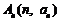 、
、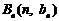 、
、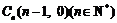 ,满足向量
,满足向量
 与向量
与向量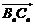 共线,且点
共线,且点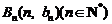 都在斜率为6的同一条直线上.
都在斜率为6的同一条直线上.
(1)试用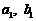 与n来表示
与n来表示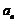 ;
;
(2)设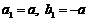 ,且12<a≤15,求数列
,且12<a≤15,求数列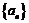 中的最小值的项.
中的最小值的项.
21、(本小题12分)已知双曲线C的中心在原点,抛物线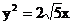 的焦点是双曲线C的一个焦点,且双曲线过点(1,
的焦点是双曲线C的一个焦点,且双曲线过点(1, 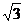 ).
).
(1)求双曲线的方程;
(2)设直线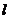 :
: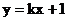 与双曲线C交于A、B两点, 试问:
与双曲线C交于A、B两点, 试问:
① 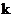 为何值时
为何值时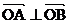
② 是否存在实数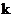 , 使A、B两点关于直线
, 使A、B两点关于直线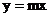 对称(
对称(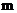 为常数), 若存在,
求出
为常数), 若存在,
求出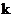 的值; 若不存在,
请说明理由.
的值; 若不存在,
请说明理由.
22、.(本小题14分) 设函数f(x)=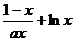 在[1+,∞
在[1+,∞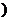 上为增函数.
上为增函数.
(1)求正实数a的取值范围.
(2)若a=1,求征: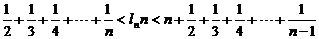
(n∈N*且n≥2)