1.已知全集U = {1,2,3,4,5,6,7},A = {3,4,5},B = {1,3,6},则A∩(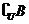 )等于 ( )
)等于 ( )
A.{4,5} B.{2,4,5,7}
C.{1,6} D.{3}
2. 若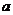 、
、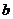 是两条不重合直线,
是两条不重合直线,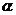 、
、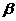 是两个不重合的平面,则
是两个不重合的平面,则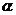 ∥
∥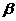 的一个充分而不必要条件是( )
的一个充分而不必要条件是( )
(A)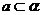 ,
,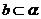 ,
,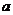 ∥
∥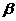 且b∥
且b∥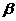 (B)
(B)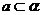 ,
,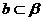 ,且a∥b
,且a∥b
(C)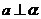 ,
,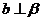 ,且
,且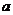 ∥
∥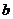 (D)
(D)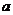 ∥
∥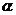 ,
,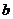 ∥
∥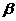 ,且a∥b
,且a∥b
3. 在等差数列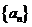 中,
中, ,
,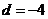 ,若
,若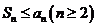 ,则
,则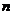 的最小值为( )
的最小值为( )
(A)60 (B)62 (C)70 (D)72
4. 已知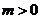 ,
,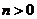 ,且满足
,且满足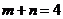 ,则下列不等式恒成立的是( )
,则下列不等式恒成立的是( )
(A)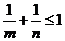 (B)
(B) (C)
(C)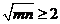 (D)
(D)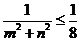
5.以直线y= -x+1与坐标轴的交点为焦点的抛物线的标准方程为( )
A x2=4y或y2=4x B x2=2y或y2=2x
C x2=-4y或y2=-4x D x2=2y或y2=-2x
6.定义:| a × b
| = | a | | b | sin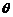 ,其中
,其中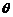 为向量a与b的夹角,若| a | = 2,| b | = 5,a ・ b = ? 6,则| a
× b | =( )
为向量a与b的夹角,若| a | = 2,| b | = 5,a ・ b = ? 6,则| a
× b | =( )
A.-8 B.
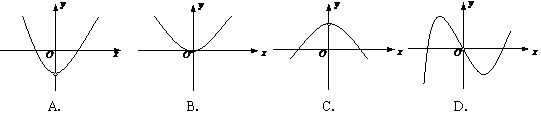
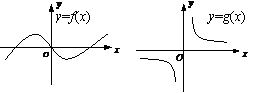 7.已知
7.已知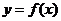 与
与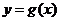 的图象如图所示,
的图象如图所示,
则函数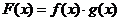 的图象可以是
的图象可以是
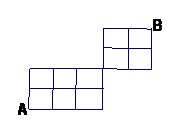
8.在某城市中,A、B两地有如右图所示道路网,从A地到B地最近的走法有( )种
A 25 B 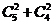 C
C 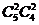 D
D 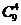
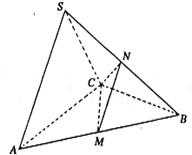
9.一个三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直,且长度分别为1,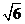 ,3,则这个三棱锥的外接球的表面积为( )
,3,则这个三棱锥的外接球的表面积为( )
(A) 16π (B) 32π (C) 36π (D) 64π
10.定义在R上的函数f(x),给出下列四个命题:
① 若f(x)是偶函数,则f(x+3)的图象关于直线x=-3对称;
② 若f(x+3)=-f(3-x),则f(x)的图象关于点(3,0)对称;
③ 若f(x+3)是偶函数,则f(x)的图象关于直线x=3对称;
④ y=f(x+3)与y=f(3-x)的图象关于直线x=3对称.
其中正确命题的个数有( )
A 0 B 1 C 2 D 3
试题卷 第 Ⅱ 卷 (非选择题,共100分)
11.设i是虚数单位,则 的虚部为 。
的虚部为 。
12. 已知变量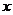 、
、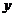 满足
满足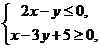 则
则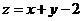 的最大值为__________。
的最大值为__________。
13.若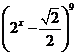 的展开式的第7项为
的展开式的第7项为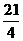 ,则
,则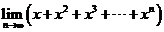

14. 已知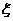 服从正态分布N(5,4),那么P(
服从正态分布N(5,4),那么P(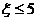 )=____________.
)=____________.
15. 对于一切实数x,令[x]为不大于x的最大整数,则函数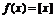 称为高斯函数或取整函数,如 f(2.1)=2;若
称为高斯函数或取整函数,如 f(2.1)=2;若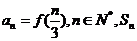 为数列
为数列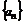 的前n项和,则
的前n项和,则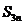 =____________.
=____________.
16.(本大题满分12分)
已知锐角△ABC中,三个内角为A、B、C,两向量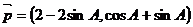 ,
,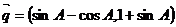 ,若
,若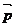 与
与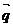 是共线向量,(1)∠A的大小;(2)求函数
是共线向量,(1)∠A的大小;(2)求函数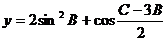 取最大值时,∠B的大小
取最大值时,∠B的大小
17. (本大题满分13分)
有A,B,C,D四个城市,它们都有一个著名的旅游点依此记为a,b,c,d把A,B,C,D和a,b,c,d分别写成左、右两列,现在一名旅游爱好者随机用4条线把左右全部连接起来,构成“一一对应”,已知连接一个城市与该城市的旅游点正确的得2分,连错的得0分;
(1)求该爱好者至少得2分的概率; (2)求所得分的数学期望?
 18.(本大题满分13分) 在三棱锥S―ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2
18.(本大题满分13分) 在三棱锥S―ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2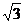 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
(1)证明:AC⊥SB;
(2)求二面角N―CM―B的大小;
(3)求点B到平面CMN的距离.
19.(本大题满分14分)
通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设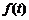 表示学生注意力随时间t (分钟)的变化规律(
表示学生注意力随时间t (分钟)的变化规律(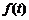 越大,表明学生注意力越集中),经过实验分析得知:
越大,表明学生注意力越集中),经过实验分析得知:
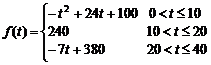
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过
适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
20.(本大题满分14分)
已知椭圆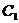 :
: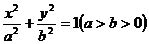 的左、右焦点分别为
的左、右焦点分别为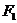 ,
,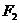 ,右顶点为A,P是椭圆
,右顶点为A,P是椭圆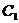 上任意一点,设该双曲线
上任意一点,设该双曲线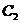 :以椭圆
:以椭圆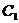 的焦点为顶点,顶点为焦点,B是双曲线
的焦点为顶点,顶点为焦点,B是双曲线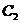 在第一象限内的任意一点,且
在第一象限内的任意一点,且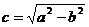 。
。
(1)设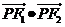 的最大值为
的最大值为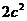 ,求椭圆离心率;(2)若椭圆离心率
,求椭圆离心率;(2)若椭圆离心率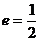 时,证明:总有
时,证明:总有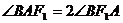 成立。
成立。
21.(本大题满分14分)
已知函数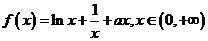 (a为实常数).
(a为实常数).
(1) 当a = 0时,求 的最小值;
的最小值;
(2)若 在
在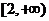 上是单调函数,求a的取值范围;
上是单调函数,求a的取值范围;
(3)设各项为正的无穷数列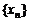 满足
满足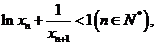 证明:
证明: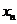 ≤1(n∈N*).
≤1(n∈N*).