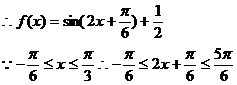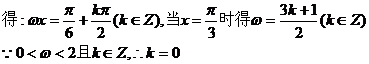17. (本小题满分12分)
解:解:
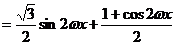 (2分)
(2分)
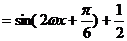 (4分)
(4分)
(Ⅰ) (6分)
(6分)
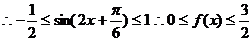 (8分)
(8分)
(Ⅱ)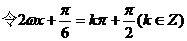 (10分)
(10分)
 (12分)
(12分)
18.(本小题满分12分)
解:(Ⅰ)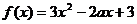 --------1分
--------1分
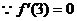 ,即27
,即27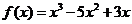 .---------2分
.---------2分
令 得
得 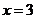 ,或
,或 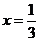 (舍去) ------------------3分
(舍去) ------------------3分
当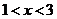 时,
时,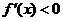 ; 当
; 当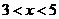 时,
时,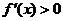 -----------------5分
-----------------5分
即当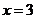 时,
时,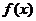 有极小值
有极小值 .又
.又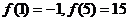
∴ f(x)在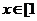 ,
,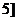 上的最小值是
上的最小值是 ,最大值是
,最大值是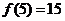 . ----------7分
. ----------7分
(Ⅱ)令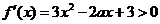 .
.
∵ x≥1. ∴ 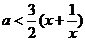 ,------------------------------------------------------9分
,------------------------------------------------------9分
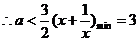 (当x=1时,取最小值).
(当x=1时,取最小值).
∴ a<3(a=3时也符合题意). ∴ a≤3.------------------------------------12分.
19.(本小题满分12分)
解:(Ⅰ)∵DE⊥平面ACD,AF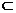 平面ACD ∴DE⊥AF
(2分)
平面ACD ∴DE⊥AF
(2分)
又∵AC=AD=CD,F为CD中点
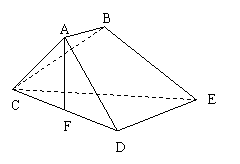 ∴AF⊥CD,又∵CD∩D∴AF⊥平面CDE
(4分)
∴AF⊥CD,又∵CD∩D∴AF⊥平面CDE
(4分)
(Ⅱ)∵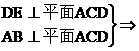 DE∥AB
DE∥AB
取DE中点M,连结AM、CM,
则四边形AMEB为平行四边形
AM∥BE,则∠CAM为AC与BE所成的角 (6分)
在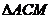 中,AC=
中,AC=
AM=
CM=
由余弦定理得,,
∴异面直线AC、BE所成的角的余弦值为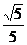 (8分)
(8分)
(Ⅲ)延长DA,EB交于点G,连结CG
因为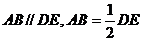 ,所以A为GD中点
(9分)
,所以A为GD中点
(9分)
又因为F为CD中点,所以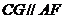 (10分)
(10分)
因为AF⊥平面CDE,所以CG⊥平面CDE
故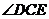 为面
为面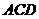 和面
和面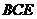 所成二面角的平面角
(11分)
所成二面角的平面角
(11分)
易求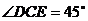 (12分)
(12分)
20. (本小题满分12分)
解:(Ⅰ) 甲得0分的概率为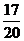 -----------------4分
-----------------4分
(Ⅱ)当乙1次赢取甲的概率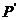 =
=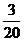 (
(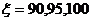 )-------------------6分
)-------------------6分
当乙2次赢取甲的概率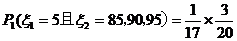 ----------8分
----------8分
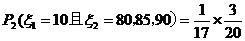 -
-
……………
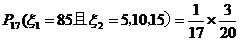 --------10分
--------10分
(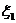 、
、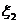 分别表示第一次、第二次转动时指针所指分数)
分别表示第一次、第二次转动时指针所指分数)
P=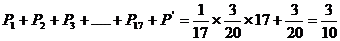 -------------------12分
-------------------12分
21. (本小题满分14分)
解:(Ⅰ) 在直线
在直线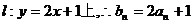 ------1分
------1分
∵P1为直线l与y轴的交点,∴P1(0,1) 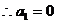 , ------2分
, ------2分
又数列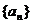 的公差为1
的公差为1 
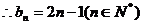 ------4分
------4分
(Ⅱ)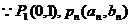
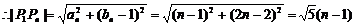 ------5分
------5分
 -----7分
-----7分
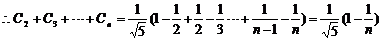 ----------8分
----------8分
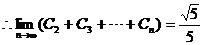 -
----------9分
-
----------9分
(Ⅲ)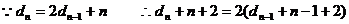 ---------12分
---------12分
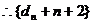 是以2为公比,4为首项的等比数列,
是以2为公比,4为首项的等比数列,
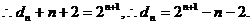 ----------------14分
----------------14分
22.(本小题满分14分)
(Ⅰ)椭圆C: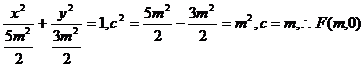 2分
2分
直线AB:y=k(x-m), 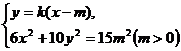 ,(10k2+6)x2-20k2mx+10k
,(10k2+6)x2-20k2mx+10k
设A(x1,y1)、B(x2,y2),则x1+x2= ,x1x2=
,x1x2=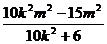 4分
4分
则xm=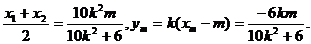 5分
5分
若存在k,使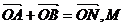 为ON的中点,∴
为ON的中点,∴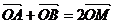 .
.
∴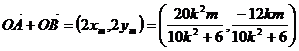 ,
,
即N点坐标为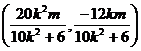 .
6分
.
6分
由N点在椭圆上,则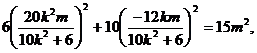 7分
7分
即5k4-2k2-3=0.∴k2=1或k2=-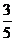 (舍).
(舍).
故存在k=±1使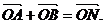 8分
8分
(Ⅱ)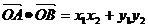 =x1x2+k2(x1-m)(x2-m)
=x1x2+k2(x1-m)(x2-m)
=(1+k2)x1x2-k
=(1+k2)・ 10分
10分
由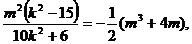 得
得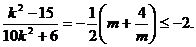 12分
12分
即k2-15≤-20k2-12,k2≤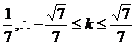 且k≠0. 14分
且k≠0. 14分