(1) 函数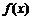 =lg(x2-2x-3)的定义域是集合M,函数
=lg(x2-2x-3)的定义域是集合M,函数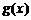 =
=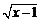 的定义域是集合P,则
的定义域是集合P,则
P∪M等于
(A)(-∞,-1)∪[1,+∞) (B)(-∞,-3)∪[1,+∞)
(C)(-3,+∞) (D)(-1,+∞)
(2) 在等比数列{an}中,a1=3,a6=24,则a16等于
(A)864 (B)1176 (C)1440 (D)1536
(3) 直线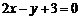 关于直线
关于直线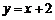 对称的直线方程是
对称的直线方程是
(A)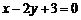 (B)
(B)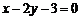
(C)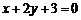 (D)
(D)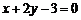
(4) 若平面α⊥平面β,l,m,n为两两互不重合的三条直线, ,α∩β=l,且m⊥n,则
,α∩β=l,且m⊥n,则
(A)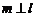 且n∥l (B)
且n∥l (B)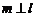 或n∥l
或n∥l
(C)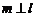 且
且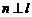 (D)
(D)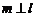 或
或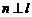
(5)
△ABC中,若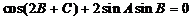 ,则△ABC一定是
,则△ABC一定是
(A)锐角三角形 (B)钝角三角形 (C)直角三角形 (D)等腰三角形
(6) 函数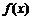 =
=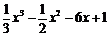 在区间(-2,2)上
在区间(-2,2)上
(A)单调递增 (B)单调递减
(C)先单调递增后单调递减 (D)先单调递减后单调递增
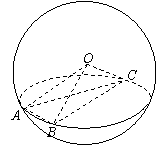 (7)
如图,已知A,B,C是表面积为48π的球面上的三点,
(7)
如图,已知A,B,C是表面积为48π的球面上的三点,
AB=2,BC=4,∠ABC=60°,O为球心,则二面角
O-AB-C的大小为
(A)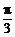 (B)
(B)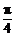
(C)arccos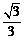 (D)arccos
(D)arccos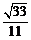
(8) 一圆形纸片的圆心为O,点Q是圆内异于O点的一定点,点A是圆周上一点,把纸片折叠使点A与点Q重合,然后抹平纸片,折痕CD与OA交于P点,当点A运动时点P的轨迹是
(A)椭圆 (B)双曲线 (C)抛物线 (D)圆
(9) 方程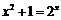 的解共有
的解共有
(A)1个 (B)2个 (C)3个 (D)4个
(10)如图,某建筑工地搭建的脚手架局部类似于4×2×3的长方体框架(由24个棱长为1个单位长度的正方体框架组合而成).一建筑工人从
A点沿脚手架到点B,每步走1个单位长度,且不连续向上攀登,则其行走的最近路线共
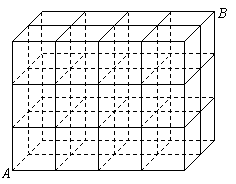 有
有
(A)150条 (B)525条
(C)840条 (D)1260条
(11)不等式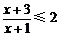 的解集为 ▲ .
的解集为 ▲ .
(12)函数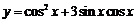 的最小正周期T= ▲ .
的最小正周期T= ▲ .
(13)过双曲线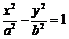 的左焦点且垂直于x轴的直线与双曲线相交于M,N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于 ▲ .
的左焦点且垂直于x轴的直线与双曲线相交于M,N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于 ▲ .
(14)已知O是△ABC内一点,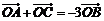 ,则△AOB与△AOC的面积的比值为 ▲ .
,则△AOB与△AOC的面积的比值为 ▲ .
(15)在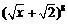 的二项展开式中,所有有理项之和为S,当x=2时,S等于 ▲ .
的二项展开式中,所有有理项之和为S,当x=2时,S等于 ▲ .
(16)已知集合A={(x,y)│|x|+|y|=2,x,y∈R},B={(x,y)│|xy|=a,x,y∈R},若A∩B中的元素所对应的点恰好是一个正八边形的八个顶点,则正数a的值为 ▲ .
(17)(本小题满分14分)
袋中装有20个不同的小球,其中有n(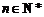 ,n>1)个红球(
,n>1)个红球(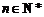 ,n>1),4个蓝球,10个黄球,其余为白球.已知从袋中取出3个颜色相同的彩球(不是白球)的概率为
,n>1),4个蓝球,10个黄球,其余为白球.已知从袋中取出3个颜色相同的彩球(不是白球)的概率为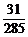 .
.
(Ⅰ)求袋中的红球、白球各有多少个?
(Ⅱ)从袋中任取3个小球,求其中一定有红球的概率.
 (18)(本小题满分14分)
(18)(本小题满分14分)
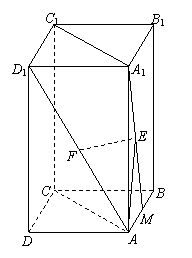
如图,在长方体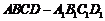 中,
中, 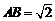 ,
,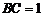 ,
,
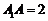 ,M为AB的中点,E,F分别为
,M为AB的中点,E,F分别为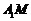 和AD1的中点.
和AD1的中点.
(Ⅰ)求证:直线EF⊥平面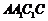 ;
;
(Ⅱ)求直线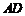 与平面
与平面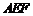 所成角的大小.
所成角的大小.
(19)(本小题满分14分)
将圆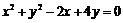 按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使
按向量a=(-1,2)平移后得到⊙O,直线l与⊙O相交于A、B两点,若在⊙O上存在点C,使 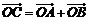 =λa,求直线l的方程及对应的点C的坐标.
=λa,求直线l的方程及对应的点C的坐标.
(20)(本小题满分14分)
已知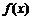 是定义在R上的函数,对于任意的实数a,b,都有
是定义在R上的函数,对于任意的实数a,b,都有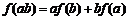 ,且
,且 .
.
(Ⅰ)求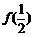 的值;
的值;
(Ⅱ)求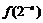 的解析式(
的解析式(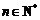 ).
).
(21)(本小题满分14分)
设函数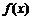 =x|x-a|+b.
=x|x-a|+b.
(Ⅰ)求证: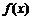 为奇函数的充要条件是a2+b2=0;
为奇函数的充要条件是a2+b2=0;
(Ⅱ)设常数b<2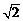 -3,且对任意x∈[0,1],
-3,且对任意x∈[0,1],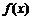 <0恒成立,求实数a的取值范围.
<0恒成立,求实数a的取值范围.
2007年南通市高三数学第二次调研测试

