1.设集合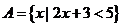 ,
,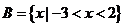 ,则
,则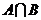 等于
等于
A.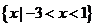 B.
B.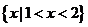
C.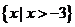 D.
D.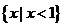
2.命题:“设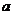 ,
,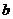 ,
,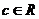 ,若
,若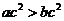 ,则
,则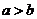 ”以及它的逆命题、否命题、逆否命题中,真命题的个数为
”以及它的逆命题、否命题、逆否命题中,真命题的个数为
A.0 B.
3.已知向量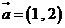 ,
,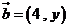 ,且
,且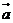 ⊥
⊥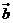 ,则
,则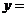
A.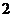 B.
B. C.
C. 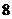 D.
D.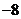
4.已知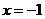 是函数
是函数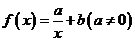 的一个零点,则函数
的一个零点,则函数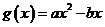 的零点是
的零点是
A.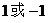 B.
B.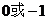 C.
C.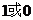 D.2或1
D.2或1
5.函数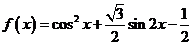 的最小正周期是
的最小正周期是
A.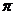 B.
B.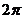 C.
C.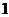 D.
D.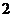
6.已知函数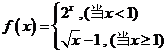 ,则
,则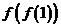 的值是
的值是
A.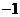 B.
B.
7.二项式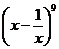 的展开式中,系数最大的项是
的展开式中,系数最大的项是
A.第5项 B.第6项 C.第5项或第6项 D.第4项或第7项
8.从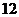 名男生和
名男生和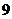 名女生中选出
名女生中选出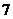 人组成一个英语社团,若按性别比例分层抽样,则不同的抽样方法有
人组成一个英语社团,若按性别比例分层抽样,则不同的抽样方法有
A.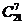 种
B.
种
B.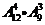 种
种
C.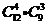 种
D.
种
D.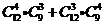 种
种
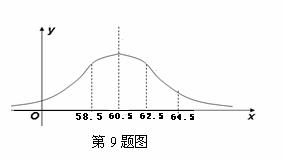
9.为了了解某地区高三男生的身体发育情况,抽查了该地区 名年龄在
名年龄在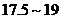 岁的高三男生的体重情况,抽查结果表明他们的体重
岁的高三男生的体重情况,抽查结果表明他们的体重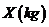 服从正态分布
服从正态分布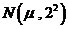 ,且正态分布密度曲线如图所示,若体重在
,且正态分布密度曲线如图所示,若体重在 属于正常情况,则这
属于正常情况,则这 名男生中属于正常情况的人数约是
名男生中属于正常情况的人数约是
A.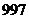 B.
B.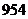 C.
C.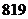 D.
D.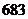
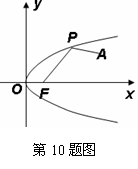
10.如图,已知点 是平面内一定点,动点
是平面内一定点,动点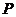 在抛物线
在抛物线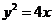 上移动,点
上移动,点 是抛物线的焦点,则
是抛物线的焦点,则 的最小值是
的最小值是
A.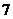 B.
B.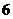 C.
C.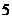 D.
D.
11.在△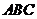 中,若
中,若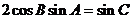 ,则△
,则△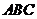 的形状一定是
的形状一定是
A.等腰直角三角形 B.直角三角形或等腰三角形
C.等腰三角形 D.直角三角形
12.已知有序实数对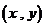 满足不等式组
满足不等式组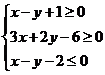 ,则目标函数
,则目标函数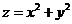 的最小值是
的最小值是
A.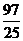 B.
B.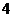 C.
C.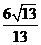 D.
D.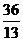
13.曲线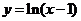 在
在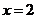 处的切线方程是_______________.
处的切线方程是_______________.
14.设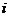 是虚数单位,且
是虚数单位,且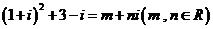 ,则
,则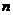 =______________.
=______________.
15.如图,类比点到直线的距离公式,平面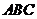 的方程可表示为
的方程可表示为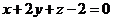 ,则点
,则点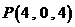 到平面
到平面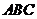 的距离是_____________.
的距离是_____________.
16.在锐角△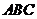 中,已知
中,已知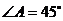 ,
,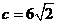 ,
,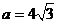 ,则
,则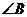 =__________.
=__________.
17.(本小题满分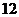 分)
分)
数列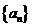 的前
的前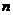 项和为
项和为 ,且
,且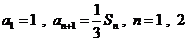 ,…,求:
,…,求:
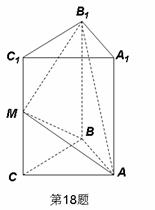 (Ⅰ)
(Ⅰ)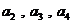 的值;
的值;
(Ⅱ)数列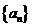 的通项公式.
的通项公式.
18.(本小题满分12分)
如图所示,在三棱柱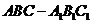 中,侧棱垂直于底面,
中,侧棱垂直于底面,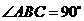 ,
,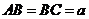 ,
,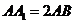 ,
,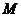 为
为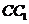 的中点.
的中点.
(Ⅰ)求证: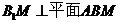 ;
;
(Ⅱ)求直线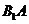 与平面
与平面 所成的角的余弦值.
所成的角的余弦值.
19.(本小题满分12分)
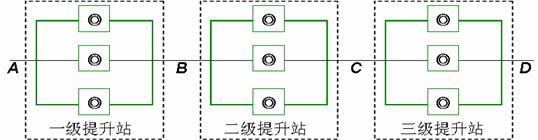
某城市的给水系统是由三级提升站组成,每级提升站由3个并列的水泵组成,每个水泵的正常运行率为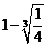 .在夜间每个提升站至少要有1台水泵能正常运行,则这个提升站才不需要紧急维修;若一个提升站的3台水泵都不能正常运行,则这个提升站需要紧急维修.
.在夜间每个提升站至少要有1台水泵能正常运行,则这个提升站才不需要紧急维修;若一个提升站的3台水泵都不能正常运行,则这个提升站需要紧急维修.
(Ⅰ)求需紧急维修的提升站数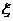 的分布列;
的分布列;
 (Ⅱ)假设每个提升站至多紧急维修1次,紧急维修1个提升站的费用为
(Ⅱ)假设每个提升站至多紧急维修1次,紧急维修1个提升站的费用为 元,求紧急维修费用
元,求紧急维修费用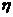 (元)的分布列和数学期望.
(元)的分布列和数学期望.
20.(本小题满分14分)
对于定义域为区间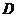 的函数
的函数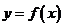 ,如果
,如果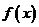 同时满足下列两个条件:
同时满足下列两个条件:
(1)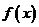 在
在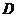 内是单调函数;
内是单调函数;
(2)存在区间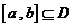
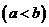 ,使得
,使得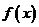 在
在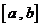 上的值域为
上的值域为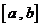 .
.
那么称函数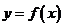 为
为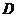 上的 “封闭函数 ”,
区间
上的 “封闭函数 ”,
区间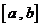 称为“封闭函数 ”的
“封闭区间”.
称为“封闭函数 ”的
“封闭区间”.
(Ⅰ)求“封闭函数
”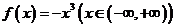 的“封闭区间”.
的“封闭区间”.
(Ⅱ)判断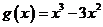 是否为
是否为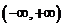 上的“封闭函数 ”,并说明理由.
上的“封闭函数 ”,并说明理由.
(Ⅲ)是否存在实数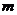 ,使函数
,使函数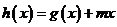 是
是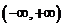 上的“封闭函数 ”?若存在,求出
上的“封闭函数 ”?若存在,求出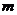 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
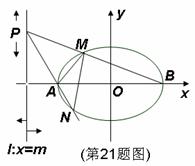 21.(本小题满分14分)
21.(本小题满分14分)
已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在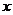 轴上,离心率
轴上,离心率
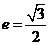 ,短半轴长
,短半轴长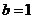 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设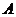 ,
,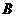 分别是椭圆
分别是椭圆 的左、右顶点,直线
的左、右顶点,直线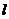 :
: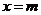 (
(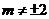 ),当点
),当点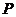 在直线
在直线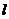 (纵坐标不为
(纵坐标不为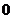 )上移动时,直线
)上移动时,直线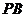 、线段
、线段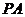 的延长线与椭圆
的延长线与椭圆 分别相交于
分别相交于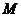 、
、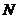 两点,且以
两点,且以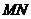 为直径的圆恒经过点
为直径的圆恒经过点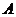 ,求
,求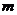 的值.
的值.
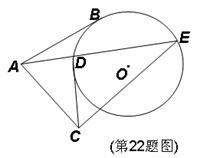 22.如图,直线
22.如图,直线 是
是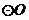 的割线,
的割线,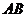 是
是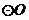 的切线,且
的切线,且
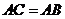 ,求证:
,求证: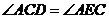 .
.
23.设直线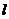 经过点
经过点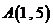 ,倾斜角为
,倾斜角为 ,圆
,圆 的方程为:
的方程为:
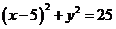 .
.
(Ⅰ)求直线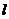 的参数方程;
的参数方程;
(Ⅱ)以直角坐标系的原点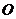 为极点,
为极点,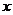 轴的正半轴为极
轴的正半轴为极
轴建立极坐标系,求圆 的极坐标方程.
的极坐标方程.
24.已知:不等式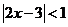 的解集为
的解集为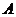 ,不等式
,不等式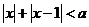 的解集为
的解集为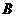 ,若
,若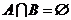 ,试求实数
,试求实数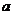 的取值范围.
的取值范围.
海口市2007年高考适应性测试