1.设集合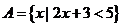 ,
,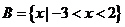 ,则
,则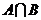 等于
等于
A.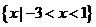 B.
B.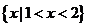
C.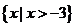 D.
D.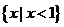
2.命题:“设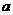 ,
,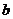 ,
,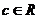 ,若
,若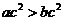 ,则
,则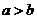 ”以及它的逆命题、否命题、逆否命题中,真命题的个数为
”以及它的逆命题、否命题、逆否命题中,真命题的个数为
A.0 B.
3.已知向量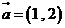 ,
,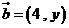 ,且
,且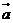 ⊥
⊥ ,则
,则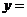
A.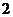 B.
B.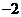 C.
C. 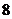 D.
D.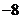
4.已知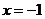 是函数
是函数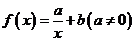 的一个零点,则函数
的一个零点,则函数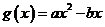 的零点是
的零点是
A.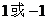 B.
B.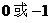 C.
C.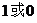 D.
D. 或2
或2
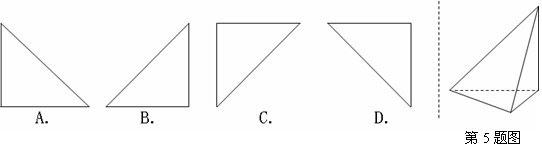 5.某几何体的斜二侧画法的直观图如图所示,它的三视图的三个视图是全等的等腰直角三角形,则它的俯视图是
5.某几何体的斜二侧画法的直观图如图所示,它的三视图的三个视图是全等的等腰直角三角形,则它的俯视图是
6.在等比数列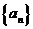 中,如果
中,如果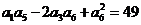 ,那么
,那么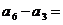
A.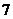 B.
B. C.
C.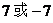 D.
D.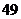
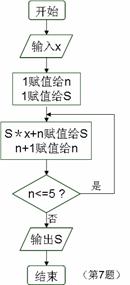
7.若x=2,则图中的程序框图执行后输出的结果是
A. 19
B.
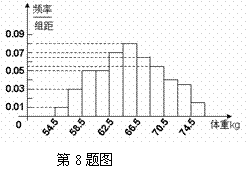
8.为了了解海口地区高三男生的身体发育情况,抽查了该地区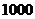 名年龄在
名年龄在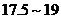 岁的高三男生的体重,根据抽查结果,绘制的频率分布直方图如图所示,若体重在
岁的高三男生的体重,根据抽查结果,绘制的频率分布直方图如图所示,若体重在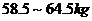 属于正常情况,则这
属于正常情况,则这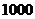 名男生中属于正常情况的人数是
名男生中属于正常情况的人数是
A.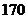 B.
B.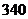 C.
C.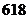 D.
D.
9.已知椭圆的中心在原点,离心率 ,且它的一个焦点为
,且它的一个焦点为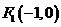 ,则此椭圆的标准方程是
,则此椭圆的标准方程是
A.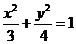 B.
B.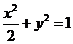 C.
C.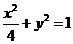 D.
D.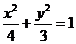
10.已知函数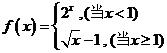 ,则
,则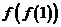 的值是
的值是
A.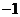 B.
B.
11. 函数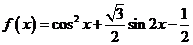 的最小正周期是 (
)
的最小正周期是 (
)
A. B.
B.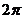 C.
C. D.
D.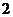
12.已知有序实数对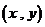 满足不等式组
满足不等式组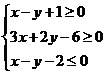 ,则目标函数
,则目标函数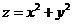 的最小值是
的最小值是
A.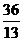 B.
B.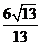 C.
C.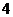 D.
D.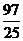
13.曲线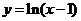 在
在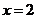 处的切线方程是_______________.
处的切线方程是_______________.
14.设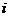 是虚数单位,且
是虚数单位,且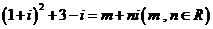 ,则
,则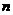 =______________.
=______________.
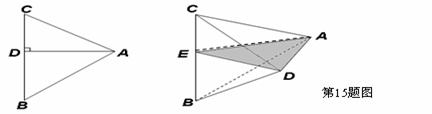
15.类比求三角形面积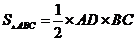 的方法,求得四面体的体积
的方法,求得四面体的体积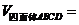
(直线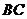 ⊥平面
⊥平面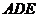 ).
).
16.在数列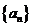 中,已知
中,已知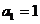 ,
, ,则
,则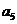 =__________.
=__________.
17.(本小题满分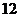 分)
分)
已知△ 的三个内角
的三个内角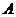 ,
,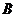 ,
, 所对的边分别为
所对的边分别为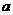 ,
,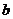 ,
,  .
.
若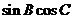

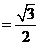 ,且
,且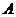 为钝角.
为钝角.
(Ⅰ)求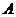 的值;
的值;
(Ⅱ)若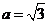 ,
,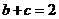 ,求
,求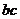 .
.
18.(本小题满分12分)
箱子里有大小相同的5个球,其中2个是红球,3个是白球,从中任意选取2个球.
(Ⅰ)求红球、白球都有的概率;
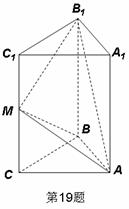 (Ⅱ)规定:若红球个数不少于白球个数则中奖,求中奖的概率.
(Ⅱ)规定:若红球个数不少于白球个数则中奖,求中奖的概率.
19. (本小题满分12分)
如图,在三棱柱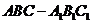 中,侧棱垂直于底面,
中,侧棱垂直于底面,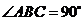 ,
,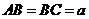 ,
,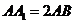 ,
,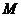 为
为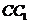 的中点.
的中点.
(Ⅰ)求证: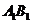 ∥
∥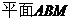 ;
;
(Ⅱ)求证: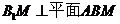 .
.
20.(本小题满分14分)
已知圆 经过
经过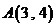 和
和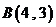 两点,且圆心
两点,且圆心 在直线
在直线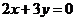 上,直线
上,直线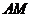 和
和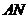 与圆
与圆 分别相交于相异的两点
分别相交于相异的两点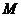 ,
,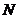 .
.
(Ⅰ)求圆 的方程;
的方程;
(Ⅱ)当直线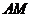 与
与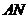 的倾斜角互补时,直线
的倾斜角互补时,直线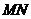 的斜率是否为一个常数,如果是常数,求出其值;如果不是常数,请说明理由.
的斜率是否为一个常数,如果是常数,求出其值;如果不是常数,请说明理由.
21. (本小题满分14分)
已知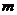 为实数,函数
为实数,函数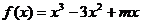 .
.
(Ⅰ)当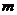 =-9时,求函数
=-9时,求函数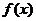 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数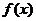 在(-
在(-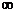 ,+
,+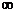 )上为增函数,试求
)上为增函数,试求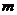 的取值范围.
的取值范围.
(Ⅲ)在(Ⅱ)条件下,若函数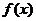 在[
在[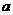 ,
,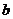 ]
]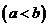 上的值域也为[
上的值域也为[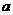 ,
,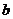 ],试求
],试求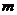 的取值范围.
的取值范围.
22.如图,直线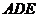 是
是 的割线,
的割线,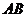 是
是 的切线,且
的切线,且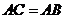 ,求证:
,求证: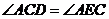 .
.
23.设直线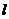 经过点
经过点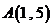 ,倾斜角为
,倾斜角为 ,圆
,圆 的方程为:
的方程为: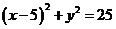 .
.
(Ⅰ)求直线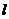 的参数方程;
的参数方程;
(Ⅱ)以直角坐标系的原点 为极点,
为极点,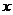 轴的正半轴为极轴建立极坐标系,求圆
轴的正半轴为极轴建立极坐标系,求圆 的极坐标方程.
的极坐标方程.
海口市2007年高考适应性测试数学(文科)