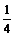11.把函数f (x) = lg(1? x) 的图象按向量a = (?1 ,0 )平移, 所得图象的函数解析式是= .
12. 在△ABC中, |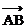 | = 2, |
| = 2, |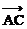 | = 3 , |
| = 3 , |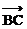 | =
| =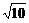 , 则cosA= .
, 则cosA= .
13. 若数列 的通项公式
的通项公式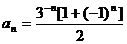 ,(n∈N*),则该数列的前n项和Sn = 。
,(n∈N*),则该数列的前n项和Sn = 。
14.关于函数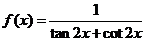 ,有下列命题:①周期是
,有下列命题:①周期是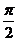 ;②
;②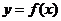 的图像关于直线
的图像关于直线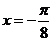 对称;③
对称;③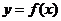 的图像关于点(
的图像关于点(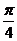 ,0)对称;④在区间
,0)对称;④在区间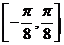 上单调递减。其中正确命题的序号是 .
上单调递减。其中正确命题的序号是 .
三. 解答题: 本大题有6小题, 每小题14分,共84分. 解答应写出文字说明, 证明过程或演算步骤.
15. (本小题满分14分)
设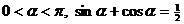 , 求
, 求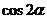 的值.
的值.
16. (本小题满分14分)
已知数列{an}的前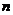 项和Sn= n (2n?1),(n∈N*)
项和Sn= n (2n?1),(n∈N*)
(1) 证明数列{an}为等差数列;
(2) 设数列{bn}
满足bn=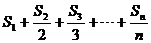 (n∈N*), 试判定: 是否存在自然数n, 使得bn = 900,若存在, 求出n的值;若不存在,说明理由;
(n∈N*), 试判定: 是否存在自然数n, 使得bn = 900,若存在, 求出n的值;若不存在,说明理由;
17.(本小题满分14分)
某电信服务点有连成一排的7座电话亭,此时全都空着,现有2位陌生人各随机选择不同的一座电话亭打电话.
(1) 求这2人选择的电话亭相隔数的分布律和期望;
(2) 若电信管理员预言这2人之间至少相隔2座电话亭,求:管理员预言为真的概率.
18 . (本小题满分14分)
设A = {x | x ¹ kp +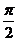 , k ÎZ }, 已知a = ( 2cos
, k ÎZ }, 已知a = ( 2cos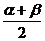 , sin
, sin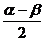 ), b = (cos
), b = (cos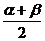 , 3sin
, 3sin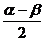 ), 其中 a, b Î A,
), 其中 a, b Î A,
(1) 若
a+b = 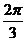 , 且a =2
b,求a, b的值。
, 且a =2
b,求a, b的值。
(2) 若a・b = 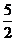 , 求tanatanb的值.
, 求tanatanb的值.
19. (本小题满分14分)
(1)若f (? 2 ) = 0,求 的表达式;
的表达式;
(2)在(1)的条件下,解不等式1 £ | F ( x ) | £ 2;
(3)设mn < 0 , m + n > 0 , 试判断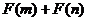 能否大于0 ?
能否大于0 ?
20. (本小题满分14分)
已知一列非零向量 ,nÎN*, 满足:
,nÎN*, 满足:
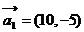 ,
,  ,(n ³ 2 ).,其中k是非零常数。
,(n ³ 2 ).,其中k是非零常数。
(1)求数列{| |}是的通项公式;
|}是的通项公式;
(2)求向量
 与
与 的夹角;
的夹角;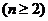 ;
;
(3)当k =  时,把
时,把 ,
, ,
, ,
,  ,
, 中所有与
中所有与 共线的向量按原来的顺序排成一列,记为
共线的向量按原来的顺序排成一列,记为 ,
, ,
, ,
,  ,
,  , 令
, 令 =
= ,O为坐标原点,求点列{Bn}的极限点B的坐标。(注:若点坐标为
,O为坐标原点,求点列{Bn}的极限点B的坐标。(注:若点坐标为 ,且
,且 ,
, ,则称点B(t,s)为点列的极限点.)
,则称点B(t,s)为点列的极限点.)
2007年杭州市第一次高考科目教学质量检测
数学试题卷(理科)评分标准
一. 选择题 : 本大题共10小题, 每小题5分, 共50分. 化
题号
1
2
3
4
5
6
7
8
9
10
答案
B
C
A
B
C
B
D
C
D
A
15. (本小题满分14分)
由cosa + sina = , 得 2sinacosa = sin2a =
, 得 2sinacosa = sin2a =  < 0,
---5分
< 0,
---5分
又由 0< a< p, 得p < 2a < , --
4分
, --
4分
∴cos2a= ? ,
--- 5分
,
--- 5分
16. (本小题满分14分)
(1) 当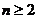 时,
时, = 4n ? 3 ,---
4分
= 4n ? 3 ,---
4分
当n = 1 时, a1 = S1 = 1, 适合. ∴a n =4n ? 3 , --- 2分
∵ ,所以
,所以 为等差数列.
--- 2分
为等差数列.
--- 2分
(2)∵  ,
--- 2分
,
--- 2分
∴bn= , ---2分,
, ---2分,
由n2 = 900, 得 n = 30, 即存在满足条件的自然数, 且n =30. ---2分
17.(本小题满分14分)
分布律
X
0
1
2
3
4
5
P
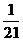
--- 每格1分, 全对8分.
期望 E (X) = 0´ +1´
+1´ +2´
+2´ +3´
+3´ +4´
+4´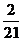 +5´
+5´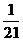 =
=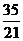 » 1.67, --- 3分
» 1.67, --- 3分
预言为真的概率P {X³2} =  +
+ +
+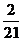 +
+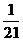 =
=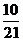 » 0.476. ---
3分
» 0.476. ---
3分
或 P {X³2} = 1 ?  ?
? =
=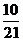 » 0.476.
» 0.476.
18 . (本小题满分14分)
(1) ∵ a+b = 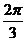 ,
,
∴a = ( 1, sin(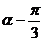 )), b = (
)), b = (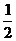 , 3sin(
, 3sin(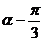 )),
--- 4分
)),
--- 4分
由a=2
b,得sin(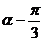 ) = 0,
) = 0,
∴a = kp +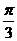 , b = ? kp +
, b = ? kp +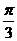 , k ÎZ.
--- 3分
, k ÎZ.
--- 3分
(2) ∵a・b = 2cos2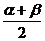 + 3sin2
+ 3sin2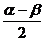 = 1 + cos (a+b) +3
= 1 + cos (a+b) +3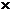
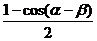
=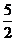 + cos (a+b) ?
+ cos (a+b) ? 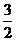 cos (a? b ) =
cos (a? b ) = 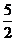 ,
--- 3分
,
--- 3分
∴ cos (a+b) =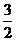 cos (a? b ),
cos (a? b ),
展开得2cosacosb ? 2sinasinb = 3cosacosb + 3sinasinb
即 ? 5sinasinb = cosacosb,
∵ a, b Î A,
∴ tanatanb= ?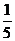 .
--- 4分
.
--- 4分
19. (本小题满分14分)
(1)∵f (? 2 ) = 0,∴ 4a + 4 = 0, 得 a = ? 1,
∴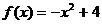 ,
,
F
( x ) = 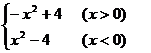 .
--- 2分
.
--- 2分
(2) ∵| F (?x ) | = | F (x ) |, ∴| F (x )|是偶函数, 故可以先求x >0的情况,
当x > 0 时, 由| F (2 )| = 0, 故当
0
< x £ 2时,
解不等式 1 £ 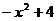 £ 2, 得
£ 2, 得 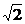 £ x £
£ x £ 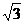 ;
;
x
> 2时, 解不等式 1 £ 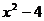 £ 2, 得
£ 2, 得 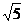 £ x £
£ x £ 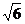 ;
;
综合上述可知原不等式的解为:
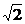 £ x £
£ x £ 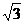 或
或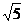 £ x £
£ x £ 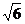 或?
或?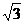 £ x £?
£ x £?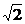 或?
或?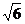 £ x £ ?
£ x £ ?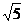 .
---6分
.
---6分
(3)∵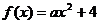 , ∴ F ( x ) =
, ∴ F ( x ) = 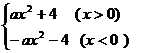 ,
,
∵ mn < 0 , 不妨设 m > 0 , 则 n < 0 , 又 m + n > 0, ∴ m > ? n > 0 , ∴m2 > n2 , ---3分
∴ F (m) + F (n) = am2 + 4 ? an2 ? 4 = a ( m2 ? n2 ) > 0.
所以: 当a
> 0 时, 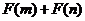 能大于0,
能大于0,
当a < 0 时,
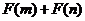 不能大于0.
---3分
不能大于0.
---3分
20. (本小题满分14分)
(1)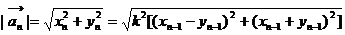 ---2分
---2分
=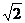 | k |
| k | 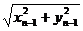 =
=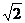 | k |
| k |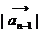 ,
, 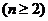 ,
,
∴{| |}是首项为5
|}是首项为5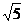 公比为
公比为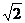 | k |的等比数列.
| k |的等比数列.
∴  = 5
= 5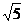 (
(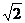 | k |)n ? 1 ---- 2分
| k |)n ? 1 ---- 2分
(2)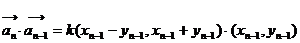 =
= = k
= k  .
.
∴cos <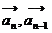 >=
>=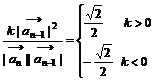 ,
---2分
,
---2分
∴当k > 0时,<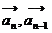 >=
>=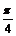 ,
,
当k < 0时,<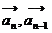 >=
>=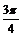 .
---2分
.
---2分
(3) 当k =  时,由(2)知: 4<
时,由(2)知: 4<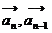 > = p,
> = p,
∴每相隔3个向量的两个向量必共线,且方向相反,
∴与向量 共线的向量为:{
共线的向量为:{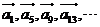 }={
}={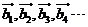 }, ---2分
}, ---2分
记 的单位向量为
的单位向量为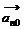 ,则
,则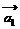 = |
= |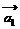 |
|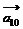 ,
,
则 = |
= | |
|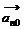 = |
= |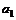 |(
|(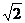 | k |)n ? 1
| k |)n ? 1 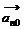 .
.
设 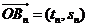 , 则 tn = 10[
, 则 tn = 10[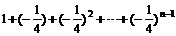 ]=10´
]=10´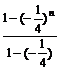 ,
,
∴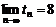 ,
,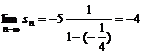 .
.
∴点列{Bn}的极限点B的坐标为( 8, ? 4 ). ---2分

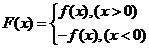
 . 13.
. 13. 14. ①
14. ①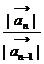
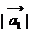 = 5
= 5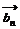 =
= 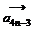 = |
= |