1. 若集合 ,
,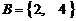 ,则“
,则“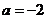 ”是“
”是“ ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2. 函数 (
(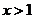 )的反函数的解析表达式为
)的反函数的解析表达式为
A. B.
B.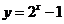
C. D.
D.
3. 已知 ,
, 为钝角,则
为钝角,则 的值为
的值为
A. B.
B. C.
C. D.
D.
4. 一家五口人:爷爷、奶奶、爸爸、妈妈和小孩坐成一排拍照片,小孩一定要紧靠在爷爷和奶奶中间坐,奶奶不坐在两端,共有不同的坐法
A. 种
B.
种
B. 种
C.
种
C. 种 D.
种 D. 种
种
5. 一个与球心距离为 的平面截球所得圆的面积为
的平面截球所得圆的面积为 ,则球的表面积为
,则球的表面积为
A.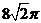 B.
B.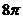 C.
C.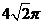 D.
D.
6. 设变量 ,
,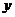 满足约束条件
满足约束条件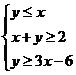 ,则目标函数
,则目标函数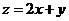 的最小值为
的最小值为
A.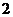 B.
B.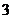 C.
C. D.
D.
7.以抛物线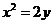 上点
上点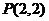 为切点的切线,与其准线交点的横坐标为
为切点的切线,与其准线交点的横坐标为
A.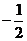 B.
B.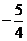 C.
C.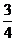 D.
D.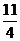
8. 将函数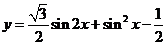 的图象进行下列哪一种变换就变为一个奇函数的图象
的图象进行下列哪一种变换就变为一个奇函数的图象
A.向左平移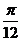 个单位
B.向左平移
个单位
B.向左平移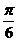 个单位
个单位
C.向右平移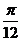 个单位
D.向右平移
个单位
D.向右平移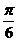 个单位
个单位
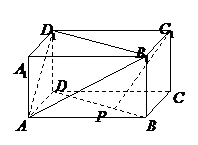 9. 在长方体
9. 在长方体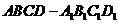 中,
中,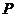 为
为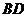 上任意一点,则一定有
上任意一点,则一定有
A.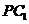 与
与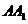 异面
B.
异面
B.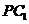 与
与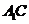 垂直
垂直
C.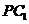 与平面
与平面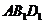 相交 D.
相交 D.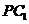 与平面
与平面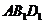 平行
平行
8
3
4
1
5
9
6
7
2
10. 将 个正整数
个正整数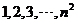 填入
填入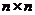 方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做
方格中,使其每行、每列、每条对角线上的数的和都相等,这个正方形叫做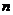 阶幻方.记
阶幻方.记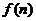 为
为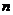 阶幻方对角线上数的和,如右图就是一个
阶幻方对角线上数的和,如右图就是一个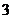 阶幻方,可知
阶幻方,可知 .已知将等差数列:
.已知将等差数列: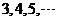 前
前 项填入
项填入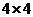 方格中,可得到一个
方格中,可得到一个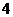 阶幻方,则其对角线上数的和等于
阶幻方,则其对角线上数的和等于
A.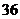 B.
B.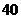 C.
C.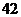 D.
D.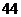
11. 某地区有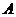 、
、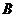 、
、 三家养鸡场,养鸡的数量分别是
三家养鸡场,养鸡的数量分别是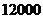 、
、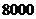 、
、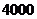 只,为了预防禽流感,现用分层抽样的方法从中抽取一个容量为
只,为了预防禽流感,现用分层抽样的方法从中抽取一个容量为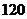 只的样本检查疫情,则应从
只的样本检查疫情,则应从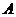 、
、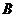 、
、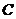 三家养鸡场分别抽取的个体数为 ▲ , ▲ , ▲ .
三家养鸡场分别抽取的个体数为 ▲ , ▲ , ▲ .
12.  ▲ .
▲ .
13. 某公司一年需购买某种货物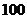 吨,每次都购买
吨,每次都购买 吨,运费为
吨,运费为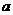 万元/次,一年的总存储费用为
万元/次,一年的总存储费用为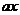 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则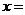 ▲ 吨.
▲ 吨.
14. 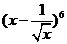 展开式中的常数项是 ▲ .(用数字作答)
展开式中的常数项是 ▲ .(用数字作答)
15.某人射击一次击中目标的概率为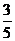 ,经过
,经过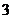 次射击,此人至少有两次击中目标的
次射击,此人至少有两次击中目标的
概率为 ▲ . (用分数表示)
16. 以下四个关于圆锥曲线的命题中
①过圆内一点(非圆心)作圆的动弦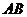 ,则
,则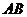 中点的轨迹为椭圆;
中点的轨迹为椭圆;
②设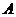 、
、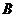 为两个定点,若
为两个定点,若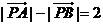 ,则动点
,则动点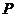 的轨迹为双曲线的一支;
的轨迹为双曲线的一支;
③方程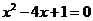 的两个根可分别作为椭圆和双曲线的离心率;
的两个根可分别作为椭圆和双曲线的离心率;
④无论方程 表示的是椭圆还是双曲线,它们都有相同的焦点.
表示的是椭圆还是双曲线,它们都有相同的焦点.
其中真命题的序号为 ▲ . (写出所有真命题的序号).
17.(本题满分12分)
在 中,
中,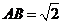 ,
,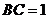 ,
, .
.
(1)求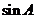 的值;(2)求
的值;(2)求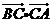 的值.
的值.
18.(本题满分14分)
已知双曲线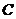 的中心在原点,焦点在
的中心在原点,焦点在 轴上,一条准线方程为
轴上,一条准线方程为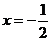 ,一条渐近线的倾斜角为
,一条渐近线的倾斜角为 .
.
(1)求双曲线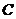 的方程;
的方程;
(2)已知直线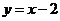 与
与 轴交于
轴交于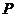 点,与双曲线
点,与双曲线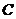 交于
交于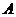 、
、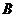 两点,求
两点,求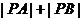 的值.
的值.
19.(本题满分14分)
如图: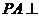 平面
平面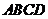 ,四边形
,四边形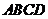 是矩形,
是矩形,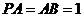 ,
,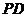 与平面
与平面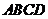 所成的角是
所成的角是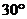 ,点
,点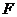 是
是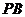 的中点,点
的中点,点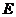 在边
在边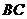 上移动.
上移动.
 (1)当点
(1)当点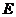 为
为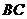 的中点时,试判断
的中点时,试判断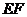 与平面
与平面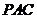 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)证明:不论点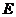 在边
在边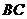 上何处,都有
上何处,都有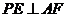 ;
;
(3)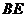 等于何值时,二面角
等于何值时,二面角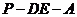 的大小为
的大小为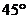 .
.
20.(本题满分16分)
已知二次函数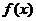 的二次项系数为
的二次项系数为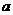 ,且不等式
,且不等式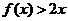 的解集为
的解集为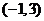 .
.
(1)若方程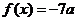 有两个相等的实数根,求
有两个相等的实数根,求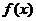 的解析式;
的解析式;
(2)若函数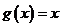
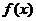 在区间
在区间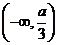 内单调递减,求
内单调递减,求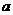 的取值范围;
的取值范围;
(3)当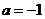 时,证明方程
时,证明方程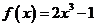 仅有一个实数根.
仅有一个实数根.
21.(本题满分14分)
设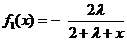 (
( 为常数,且
为常数,且 ),
),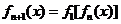 ,
,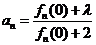 ,(
,(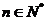 ).
).
(1)求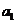 的值;
的值;
(2)求证:数列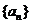 是等比数列;
是等比数列;
(3)设数列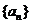 的前
的前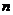 项和为
项和为 ,
, ,
,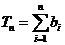 ,试比较
,试比较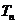 与
与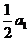 的大小.
的大小.

