1、函数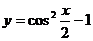 的最小正周期为
的最小正周期为
A.4π
B.2π
C.π
D.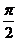
2、己知集合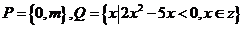 ,若
,若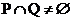 ,则m等于
,则m等于
A.1
B. D.1或2
D.1或2
3、已知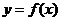 存在反函数
存在反函数 ,若
,若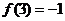 ,则函数
,则函数 的图像一定经过的一个点是
的图像一定经过的一个点是
A.(-2,3) B.(2,-1) C.(0,3) D.(4,-1)
4、设实数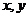 满足
满足 ,则
,则 的最小值为
的最小值为
A. B.
B. C.4
D.8
C.4
D.8
5、已知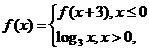 ,则f(-9)等于
,则f(-9)等于
A.-1 B.0 C.1 D.3
6、已知a, b, c, d成等比数列,则下列三个数:①a+b , b+c, c+d; ②ab, bc, cd; ③a-b, b-c, c-d中,必成等比数列的个数为
A.3 B.2 C.1 D.0
7、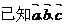 是三个非零向量,则下列命题中真命题的个数为
是三个非零向量,则下列命题中真命题的个数为
(1) ; (2)
; (2)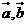 反向
反向 ;
;
(3) ; (4)
; (4)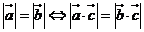
A.1 B.2 C.3 D.4
8、设 是等差数列
是等差数列 前n项和,已知
前n项和,已知 ,则
,则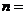
A.15 B.16 C.17 D.18
9、一圆与直线 相切于点(1,-2),且圆心在直线
相切于点(1,-2),且圆心在直线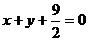 上,则圆的方程为
上,则圆的方程为
A.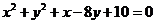 B.
B.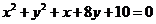
C. D.
D.
10、将函数 的图像按向量
的图像按向量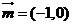 平移后,得到函数
平移后,得到函数 的图像C,若曲线C关于原点对称,那么实数a 的值是
的图像C,若曲线C关于原点对称,那么实数a 的值是
A.-1 B.-3 C.0 D.1
11、若 表示
表示 的区间长度,函数
的区间长度,函数 的值域区间长度为2(
的值域区间长度为2( ),则实数a的值为
),则实数a的值为
A.4 B.2 C. D.1
D.1
12、做一个面积为1m2,形状为直角三角形的铁架框,用下列四种长度的铁管,最合理(够用,且浪费最少)的是
A.4.6m B.4.8m C.5m D.5.2m
第Ⅱ卷(非选择题,共90分)
13、若A(1, ),B(-3,-
),B(-3,- ),直线
),直线 过原点,且与线段AB有公共点,则直线
过原点,且与线段AB有公共点,则直线 倾斜角的范围是
。
倾斜角的范围是
。
14、在△ABC中,∠A=60°,BC=2,则△ABC的面积的最大值为 。
15、已知y=loga(2-ax)在[0,1]上是 的减函数,则函数f(x)=x2-ax+1在[0,1]上的最大值为
。
的减函数,则函数f(x)=x2-ax+1在[0,1]上的最大值为
。
16、数列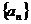 的构成法则如下:
的构成法则如下: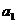 =1,如果
=1,如果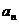 -2为自然数且之前未出现过,则用递推公式
-2为自然数且之前未出现过,则用递推公式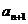 =
=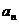 -2,否则用递推公式
-2,否则用递推公式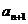 =3
=3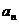 ,则
,则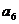 =
。
=
。
17、(本小题满分12分)
已知函数
(1)求函数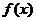 的最小正周期和最大值及相应的
的最小正周期和最大值及相应的 取值;
取值;
(2)当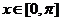 时,求函数
时,求函数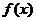 的单调递减区间;
的单调递减区间;
(3)函数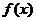 的图象可由y=sin x的图象经过怎样的变换得到?
的图象可由y=sin x的图象经过怎样的变换得到?
18、(本小题满分12分)
已知正项数列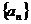 的前n项和为
的前n项和为 ,且满足
,且满足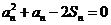
(1)求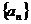 的通项公式;
的通项公式;
(2)若b1=1,2bn-bn-1=0(n≥2,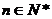 ),cn=anbn,求
),cn=anbn,求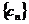 的前n项和为Tn。
的前n项和为Tn。
19、(本小题满分12分)
已知函数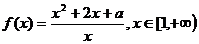
(1)当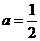 时,求函数
时,求函数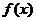 的最小值;
的最小值;
(2)若对任意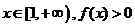 恒成立,试求实数a的取值范围
恒成立,试求实数a的取值范围
20、(本小题满分12分)
直线x+y=a与圆x2+y2=1交于A(x1, y 1),B(x 2,
y 2),O为坐标原点,是否存在实数a使 ?若存在,求出a;若不存在,说明理由。
?若存在,求出a;若不存在,说明理由。
21、(本小题满分12分)已知方程x2+y2-2x-4y+m=0
(1)若此方程表示圆,求 m的取值范围;
(2)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM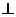 ON(O为坐标原点),求m的值;
ON(O为坐标原点),求m的值;
(3)在(2)的条件下,求以MN为直径的圆的方程。
22、(本小题满分14分)对于函数f(x)=ax2+(b+1)x+b-2(a≠0),若存在实数x0,使f(x0)= x0成立,则称x0为f(x)的不动点。
(1)当a=2,b=-2时,求f(x)的不动点;
(2)若对于任何实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围;
(3)在(2)的条件下,若y=f(x)的图象上A、B两点的横坐标是函数f(x)的不动点,且直线 是线段AB的垂直平分线,求实数b的取值范围
是线段AB的垂直平分线,求实数b的取值范围

