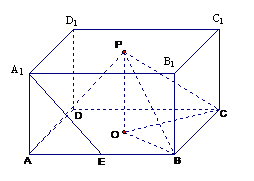
1.如图阴影部分所表示的集合是
A.CIA∩B B.A∩CIB
C.CIA∪B D.A∪CIB
2.已知点P为圆x2+y2-2x+2y=0的圆心,则点P到直线x-y+1=0的距离是
A.  B.
B.  C.
C.  D.
D.
3.设f(x)= ,则f[f(
,则f[f( )]=
)]=
A.  B.
B. C.-
C.- D.
D. 
4.设x,y满足不等式组 则z=3x-2y的最大值是
则z=3x-2y的最大值是
A.0 B.
5.已知抛物线y2=8x,定点A(3,2),F为焦点,P为抛物线上的动点,则|PF|+|PA|的最小值为
A.5 B.6 C.7 D.8
6.已知△ABC,若对任意t∈R,≥,则
A.∠A=900 B.∠B=
7.已知直线 是函数
是函数 图象的一条对称轴,则函数
图象的一条对称轴,则函数 图象的一条对称轴方程是
图象的一条对称轴方程是
A. B.
B. C.
C. D.
D.
8.已知数列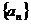 的通项
的通项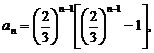 则下列表述正确的是
则下列表述正确的是
A .最大项为0,最小项为
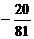 B.最大项为0,最小项不存在
B.最大项为0,最小项不存在
C.最大项不存在,最小项为
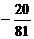 D.最大项为0,最小项为
D.最大项为0,最小项为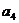
9.已知三棱锥S-ABC的底面是正三角形,点A在侧面SBC上的射影H是△SBC的垂心,SA=a,则此三棱锥体积最大值是
A.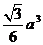 B.
B.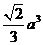 C.
C. D.
D.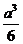
10.将9个学生分配到甲、乙、丙三个宿舍,每宿舍至多4人(床铺不分次序),则不同的分配方法有
A.3710
B.
11.在平行四边形ABCD中, =a,
=a,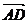 =b,
=b,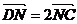 ,M为BC的中点,则
,M为BC的中点,则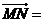
▲ .(用a,b表示)。
12.不等式3-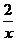 <x的解集是 ▲ .
<x的解集是 ▲ .
13.若在(x+1)4(ax-1)2的展开式中,x3的系数是20,则a=___▲______.
14.椭圆 与直线
与直线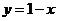 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为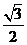 ,则 值 = ▲ .
,则 值 = ▲ .
15.在△ABC中,cosB为sinA、sinC的等比中项,sinB为cosA、cosC的等差中项,则∠B= ▲ .
16. 给出下列四个命题:
①过平面外一点,作与该平面成θ角的直线一定有无穷多条。
②一条直线与两个相交平面都平行,则它必与这两个平面的交线平行;
③对确定两条异面直线,过空间任意一点有且只有唯一的一个平面与这两条异面直线都平行;
④对两条异面的直线,都存在无穷多个平面与这两条直线所成的角相等;
其中正确的命题序号为: ▲ 。
17.(本小题满分12分)
设双曲线C: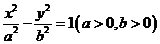 的离心率e=2,经过双曲线的右焦点F且斜率为
的离心率e=2,经过双曲线的右焦点F且斜率为 的直线交双曲线于A、B点,若
的直线交双曲线于A、B点,若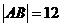 ,求此时的双曲线方程。
,求此时的双曲线方程。
18.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知函数f(x)=x3+ax2+bx+c在点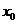 处取得极小值-5,其导函数
处取得极小值-5,其导函数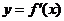
的图象经过点(0,0),(2,0),
(Ⅰ)求a,b的值; (Ⅱ)求x0及函数f(x)的表达式。
19.(本小题满分14分,第一小问满分4分,第二小问满分5分,第三小问满分5分)
如图,O,P分别是正四棱柱ABCD-A1B
(Ⅰ)求证:A1E∥平面PBC;
(Ⅱ)当k=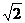 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(Ⅲ) 当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
20.(本小题满分16分,第一小问5分,第二小问满分5分,第三小问满分6分)
对于函数y=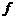 (
(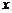 )(
)( 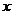
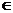 D,D为函数定义域),若同时满足下列条件:
D,D为函数定义域),若同时满足下列条件:
① f(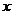 )在定义域内单调递增或单调递减;
)在定义域内单调递增或单调递减;
②
存在区间[a ,b]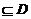 ,使
,使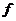 (
(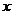 )在[a ,b]上的值域是[a ,b]。
)在[a ,b]上的值域是[a ,b]。
那么把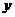 =
= 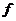 (
(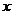 )(x
)(x 称为闭函数.
称为闭函数.
(Ⅰ) 求闭函数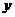 = ?
= ?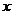 3符合条件②的区间[a,b];
3符合条件②的区间[a,b];
(Ⅱ)判定函数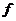 (
(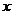 )=
)= 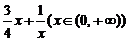 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;
(Ⅲ) 若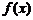 =
=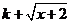 是闭函数,求实数
是闭函数,求实数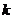 的取值范围
的取值范围
21.(本小题满分14分,第一小问满分7分,第二小问满分7分)
已知函数f(x)=x3+ax2+bx+c关于点(1,1)成中心对称,且f '(1)=0.
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)设数列{an}满足条件:a1∈(1,2),an+1=f (an)。
求证:(a1- a2)・(a3-1)+(a2- a3)・(a4-1)+…+(an- an+1)・(an+2-1)<1