1.设全集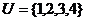 两个集合
两个集合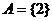 ,
,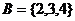 ,则
等于
,则
等于
A. {1} B. {1,3,4} C. {2} D. {3,4}
2. 在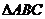 中,
中,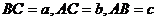 ,如果
,如果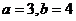 ,那么“
,那么“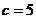 ”是“
”是“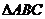 为直角三角形”的
为直角三角形”的
A.充分不必要条件 B.必要不充分条件
C. 充要条件 D.既不是充分又不是必要条件
3. 若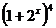 的展开式的第3项为12,则x等于
的展开式的第3项为12,则x等于
A.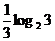 B.
B.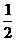 C.
C.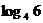 D.2
D.2
4.抛物线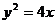 上点
上点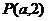 到焦点F的距离为
到焦点F的距离为
A. 1 B.
5.已知数列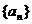 的通项公式为
的通项公式为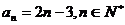 ,其前n项和为
,其前n项和为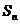 ,则使
,则使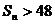 成立的n的最小值为
成立的n的最小值为
A .7 B.
6. 函数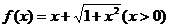 的反函数是
的反函数是
A.  B.
B.
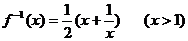
C. 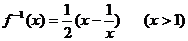 D.
D.
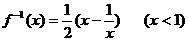
7. 已知函数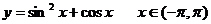 ,则下列正确的是
,则下列正确的是
A. 是偶函数,有最大值为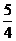 B. 是偶函数,有最小值为
B. 是偶函数,有最小值为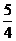
C. 是偶函数,有最大值为2 D. 是奇函数,没有最小值
8. 设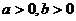 ,则以下不等式中不恒成立的是
,则以下不等式中不恒成立的是
A. 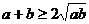 B.
B. 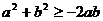
C. 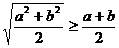 D.
D. 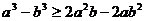
9. 如果x、y满足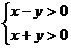 ,则有
,则有
A. 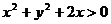 B.
B.
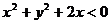
C. 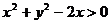 D.
D.
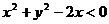
10. 已知向量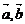 是两个不共线的非零向量, 向量
是两个不共线的非零向量, 向量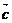 满足
满足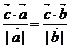 .则向量
.则向量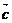 用向量
用向量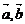 一定可以表示为
一定可以表示为
A. 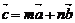 且
且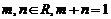 . B.
. B. 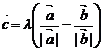
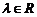
C. 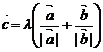
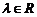
D. 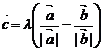
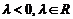 , 或
, 或 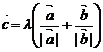
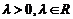
13.函数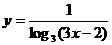 的定义域是
.
的定义域是
.
14.已知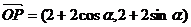 ,
,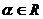 ,(O为坐标原点),向量
,(O为坐标原点),向量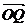 满足
满足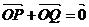 ,则动点Q的轨迹方程是
.
,则动点Q的轨迹方程是
.
15.对共有10人的一个数学小组做一次数学测验,测试题由10道单项选择题构成,每答对1题得5分,答错或不答得0分,批阅后的统计得分情况如下
得分
50分
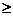 45分
45分
 40分
40分
 35分
35分
人数
2
4
8
10
则这次测试的平均成绩为 .
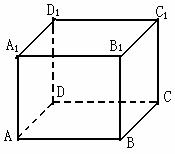 16.在正四棱柱
16.在正四棱柱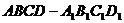 中,如果底边正方形ABCD的边长
中,如果底边正方形ABCD的边长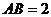 ,侧棱
,侧棱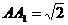 ,则下列四个命题:
,则下列四个命题:
①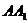 与
与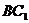 成
成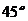 角;
角;
② 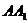 与
与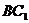 的距离为2 ;
的距离为2 ;
③ 二面角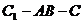 为
为 ;
;
④ 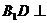 平面
平面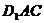 .
.
则正确命题的序号为 .
17、已知两个函数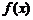 和
和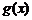 的定义域和值域都是集合{1,2,3},其定义如下表.
的定义域和值域都是集合{1,2,3},其定义如下表.
x
1
2
3
f(x)
2
3
1
x
1
2
3
g(x)
1
3
2
填写下列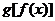 的表格
的表格
x
1
2
3
g (f(x))
18、现要给四棱锥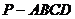 的五个面涂上颜色,要求相邻的面涂不同的颜色,可供选择的颜色共有4种,则不同的涂色方案的种数共有
种。
的五个面涂上颜色,要求相邻的面涂不同的颜色,可供选择的颜色共有4种,则不同的涂色方案的种数共有
种。
17.( 本小题满分12分)
黄种人群中各种血型的人所占的比如下表所示:
血型
A
B
AB
O
该血型的人所占/%
28
29
8
35
已知同种血型的人可以输血,O型血可以输给任一种血型的个人,任何人的血都可以输给AB型的人,其他不同血型的人不能互相输血.小明是B型血,若小明需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找两个人,当中至少有一个人,其血可以输给小明的概率是多少?
18. ( 本小题满分14分)
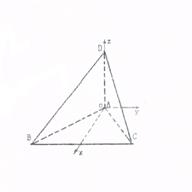
 如图,三棱锥
如图,三棱锥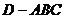 中,
中,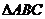 是边长为4的正三角形,
是边长为4的正三角形,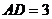 ,E为AB的中点,
,E为AB的中点, .
.
(1) 求证:平面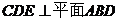 ;
;
(2) 求直线 和平面CDE所成的角的大小;
和平面CDE所成的角的大小;
(3) 求点A到平面BCD的距离.
19. ( 本小题满分14分)
已知正数数列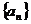 中,
中,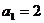 .若关于
.若关于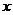 的方程
的方程
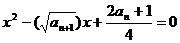
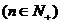 有相等的实根.
有相等的实根.
(1)求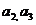 的值;
的值;
(2)求证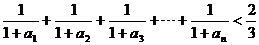
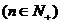 .
.
20. ( 本小题满分15分)
已知双曲线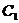 的方程为
的方程为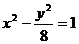 ,椭圆
,椭圆 长轴的两个端点恰好为双曲线
长轴的两个端点恰好为双曲线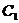 的两个焦点.
的两个焦点.
(1)如果椭圆 的两个焦点又是双曲线的两个顶点,求椭圆
的两个焦点又是双曲线的两个顶点,求椭圆 的方程;
的方程;
(2)如果椭圆 的方程为
的方程为 ,且椭圆
,且椭圆 上存在两点A,B关于直线
上存在两点A,B关于直线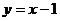 对称,求
对称,求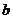 取值范围.
取值范围.
21.( 本小题满分15分)
已知函数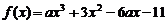 ,
,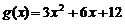 ,和直线m:
,和直线m: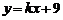 .又
.又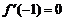 .
.
(1)求a的值;
(2)是否存在k的值,使直线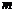 既是曲线y=f(x)的切线,又是y=g(x)
的切线;如果存在,求出k的值;如果不存在,说明理由.
既是曲线y=f(x)的切线,又是y=g(x)
的切线;如果存在,求出k的值;如果不存在,说明理由.
(3)如果对于所有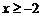 的x,都有
的x,都有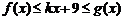 成立,求k的取值范围.
成立,求k的取值范围.
盐城市2005/2006学年度高三第二次调研考试
tx数 学 试 卷 答 案
1.D 2.A 3.B 4.B 5.C 6.C 7.A 8.D 9. A 10.C
11. 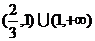 12.
12. 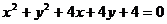 13. 42 14. ②③ 15.3,2,1 16.72
13. 42 14. ②③ 15.3,2,1 16.72
18. (1)对于任一个人,其血型为A,B,AB,O型的事件分别记为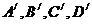 ,它们是互斥的,由已知,有
,它们是互斥的,由已知,有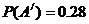 ,
,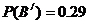
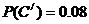
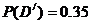
因为B,O型血可以输给B型血的人,故“可以输给B型血的人”为事件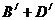
根据互斥事件的加法公式,有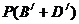 =
=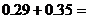
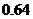 .
.
所以任何一人.其血可以输给小明的概率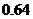
(2) 由于A,AB型血不能输给B型血的人,一个人“不能输给B型的人”为事件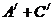
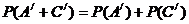 =
=
“任何两个人,其中至少有一个人,可以输给小明”的事件记为E,他的对立事件为:两个人都不能输血给小明,则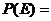
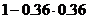 =
=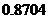 .
.
所以,任何二个人,其中至少有一个人,其血可以输给小明的概率为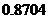
答:略
19. (1) 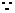
 ,
,

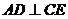 ,又
,又
 为正三角形,E为AB的中点,
为正三角形,E为AB的中点,
 而
而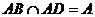

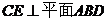 ,又
,又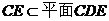

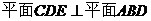
(2)由(1)得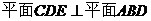 ,
, AD在平面CDE上的射影为DE
AD在平面CDE上的射影为DE
所以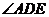 即为所成的角.
即为所成的角.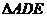 为
为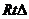 ,且AE=2,AD=3,
,且AE=2,AD=3,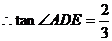

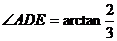 ,即直线AD与平面CDE所成的角为
,即直线AD与平面CDE所成的角为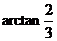
(3)取BC的中点M,连接DM,过A点在平面DAM内作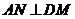 于N
于N
证得 ,所以
,所以
 AM=
AM= ,DM=
,DM=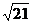 ,
,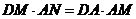 所以
所以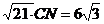
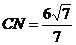
(方法2)(10建立看见直角坐标系(如图)
∵E为AB的中点,∴E点坐标为(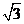 。-3,0),
。-3,0),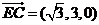
设平面CDE的法向量m=(s,t,1)
则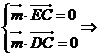
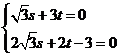 ∴
∴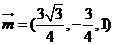
又平面ABD的法向量为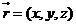 ∵
∵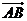 =(
=(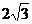 。-2,0)
。-2,0) 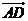 =(0,0,3)
=(0,0,3)
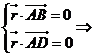
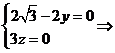
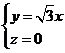 不妨设x=1,则
不妨设x=1,则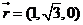
而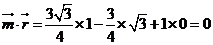 ∴
∴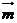 ⊥
⊥ ∴平面CDE⊥平面ABD
∴平面CDE⊥平面ABD
(2)设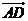 与
与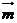 的夹角为
的夹角为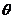 ,则cos
,则cos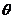 =
=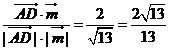
∴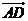 与
与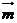 的夹角为arccos
的夹角为arccos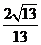 即AD与平面CDE所成的角为
即AD与平面CDE所成的角为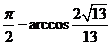
(3)则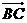 =(0,4,0),
=(0,4,0), =(2
=(2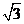 ,2,-3),
,2,-3),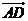 =(0,0,3)设平面BCD的法向量为
=(0,0,3)设平面BCD的法向量为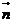 =(p,q,1)
=(p,q,1)
则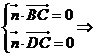

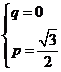 则
则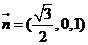
向量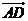 =(0,0,3)在
=(0,0,3)在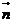 =(
=( ,0,1)上的投影为
,0,1)上的投影为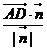 =
=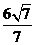
20.解:(1)由题意得 得
得 得
得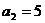 ,
,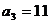
(2)由于 =
=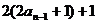 =
=
=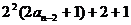 =
=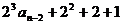 =
=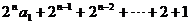 =
=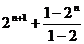 =
=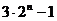

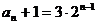
或:∵an+1=2an+1 ∴an+1+1=2(an+1) ∴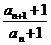 =2 ∵a1+1=2+1=3 ∴an+1=3・2n-1
=2 ∵a1+1=2+1=3 ∴an+1=3・2n-1
则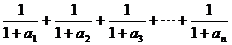 =
=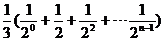
=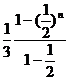 =
=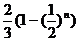
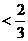 所以
所以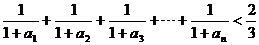
21.解(1)在双曲线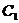 的方程
的方程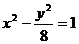 中
中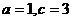 ,则椭圆
,则椭圆 方程为
方程为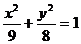
(2)椭圆 方程为
方程为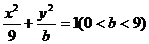 , A、B点所在直线方程设为
, A、B点所在直线方程设为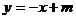 ,
,
代入椭圆 方程得
方程得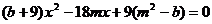
由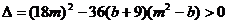 得
得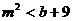 设
设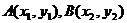 那么
那么
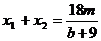 ,
, 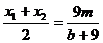 ,所以
,所以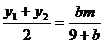
将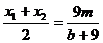 ,
,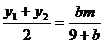
代入直线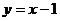 得
得 再将
再将 代入
代入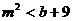 得
得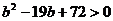 ,
,
解得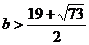 (舍去)或
(舍去)或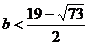 ,
,
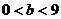

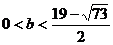
22.解:(1)因为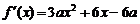 ,所以
,所以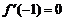 即
即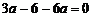 ,所以a=-2.
,所以a=-2.
(2)因为直线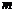 恒过点(0,9).
恒过点(0,9).
先求直线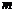 是y=g(x)
的切线.设切点为
是y=g(x)
的切线.设切点为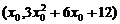 ,因为
,因为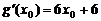 .
.
所以切线方程为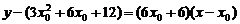 ,将点(0,9)代入得
,将点(0,9)代入得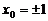 .
.
当 时,切线方程为y=9,
当
时,切线方程为y=9,
当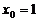 时,切线方程为y=12x+9.
时,切线方程为y=12x+9.
由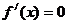 得
得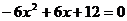 ,即有
,即有
当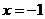 时,
时,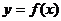 的切线
的切线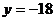 ,
,
当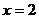 时,
时, 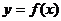 的切线方程为
的切线方程为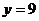

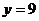 是公切线,
是公切线,
又由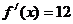 得
得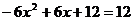

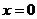 或
或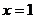 ,
,
当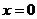 时
时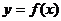 的切线为
的切线为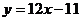 ,
,
当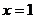 时
时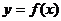 的切线为
的切线为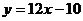 ,
,
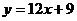 ,不是公切线
,不是公切线
综上所述 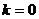 时
时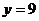 是两曲线的公切线
是两曲线的公切线
(3).(1)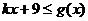 得
得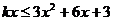 ,当
,当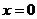 ,不等式恒成立,
,不等式恒成立,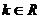 .
.
当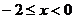 时,不等式为
时,不等式为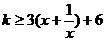 ,
,
而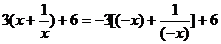
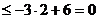
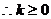
当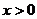 时,不等式为
时,不等式为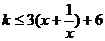 ,
,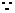
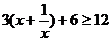

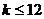
 当
当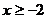 时,
时,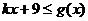 恒成立,则
恒成立,则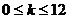
(2)由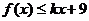 得
得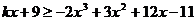
当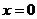 时,
时,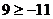 恒成立,
恒成立,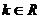 ,当
,当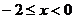 时有
时有
设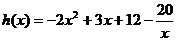 =
=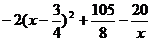 ,
,
当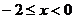 时
时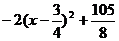 为增函数,
为增函数,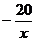 也为增函数
也为增函数

 要使
要使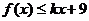 在
在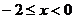 上恒成立,则
上恒成立,则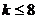
由上述过程只要考虑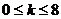 ,则当
,则当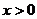 时
时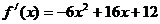 =
=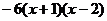
 在
在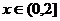 时
时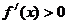 ,在
,在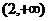 时
时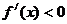

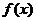 在
在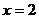 时有极大值即
时有极大值即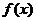 在
在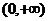 上的最大值,又
上的最大值,又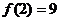 ,即
,即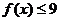 而当
而当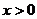 ,
,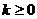 时
时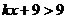 ,
,
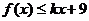 一定成立
一定成立
综上所述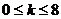 .
.

