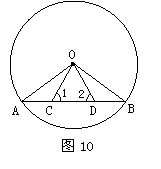
1.20的结果是
A.0
B.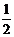
2.方程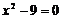 的解是
的解是
A. B.
B.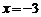 C.
C.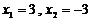 D.
D.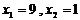
3.分式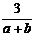 ,
,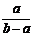 ,
,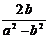 的最简公分母为
的最简公分母为
A. B.(
B.( )(
)(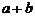 )
)
C.( )(
)(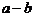 ) D.
(
) D.
( )(
)(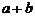 )(
)(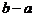 )
)
4.若一元二次方程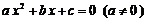 的各项系数满足
的各项系数满足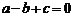 ,那么这个方程必有一根为
,那么这个方程必有一根为
A.0
B.
5. 将方程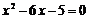 配方后所得的方程为
配方后所得的方程为
A.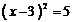 B.
B.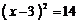 C.
C.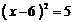 D.
D.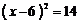
6.下面四种抽样调查选取样本的方法,你认为合适的是
①某校九年级全体298名学生参加了体育测试,为了了解达标情况,用抽签方式得到其中60名学生的测试成绩;②为了了解某校九年级全体298名学生期末考试平均成绩,抽查前60名学生的平均成绩;③为了了解海南省2006年全年的平均气温,上网查询了2006年6月份30天的气温情况;④为了了解某产品质量,检验员在上班时间在产品流水线上,每隔1小时随机地抽查了8批产品检查其质量.
A.①② B.①③ C.①④ D.②④
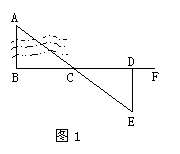
7. 小明为了测量河岸相对的两点A、B的距离,先在AB的垂线BF上取两点C、D,使得CD=BC,再取点E,使得ED⊥BF,且点A、C、E在同一条直线上(如图1),由△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,小明判定△EDC≌△ABC的理由是
A.边角边 B.角边角 C.边边边 D.斜边直角边
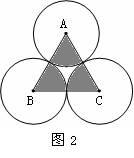
8.如图2,以等边三角形ABC的顶点为圆心的三个等圆两两外切,若△ABC的周长为12,则图中阴影部分的面积之和为
A.2π B.4π C.8π D.16π
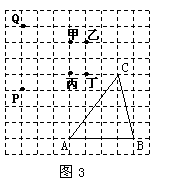
9. 如图3,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△RPQ≌△CAB,则点R只能选取甲、乙、丙、丁四点中的
A.甲 B.乙 C.甲和丙 D.乙和丁
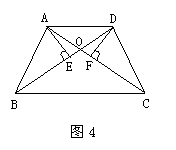
10.如图4,在梯形ABCD中,AD∥BC,AB=DC,AD≠AB,AC和BD相交于点O,AE⊥BD于E,DF⊥AC于F则图中全等三角形共有( )对
A.3
B.
11.计算 .
.
12.写出下列各式中未知的分子或分母:
(1)  ; (2)
; (2)  .
.
13.如图5,将大小完全一样的含有30°角的两块直角三角尺叠放在一起,使直角的顶点重合于点O,若A、C两点间的距离是1.5,则B、D两点间的距离为 .
14.如图6,AB是⊙O的直径,AB=6,∠D=30°,则弦BC的长为 .
15.如图7,PC切⊙O于点C,割线PBA经过圆心O,若∠ACP=110°,则∠P等于 °.
16. 如图8,某传送带的一个转动轮的半径为
17. 如图9,在△ABC和△ADC中,下列三个论断:①AB=AD,②∠ACB=∠ACD,③BC=DC. 将其中两个论断作为条件,余下的一个论断作为结论,用“如果……,那么……”的形式,写出一个真命题是 .
18.在一个不透明的袋中装有除颜色外其余都相同的红、黄、绿三种颜色的小球,其中有红球4个,黄球6个,若从该袋中随机摸出一个球,摸中红球的概率是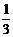 ,则该袋中有绿球
个.
,则该袋中有绿球
个.
19.(8分)先化简,再求值: 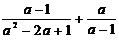 , 其中
, 其中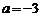 .
.
20.(10分)解下列方程.
(1)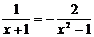 (2)
(2)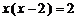
21.(8分)某商店为了了解本店罐装饮料上半年的销售情况,随机调查了8天该类饮料的日销售量,结果如下(单位:箱):31、33、29、32、25、26、31、33
(1)这8天的平均日销售量是多少箱;
(2)根据(1)中计算的结果,估计上半年(按181天计算)该店能销售这类饮料多少箱?
22.(8分)某商品经两次提价,零售价升为原来的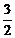 ,已知两次提价的百分率相同,求每次提价的百分率(精确到0.1%).
,已知两次提价的百分率相同,求每次提价的百分率(精确到0.1%).
23.(10分)如图10,AB是⊙O的弦(非直径),C、D是AB上的两点,且AC=BD.
求证:∠1=∠2.
24. (12分) 用两个全等的正方形ABCD和DCEF拼成一个矩形ABEF,把一个足够大的直角三角尺的直角顶点与这个矩形的边AF的中点D重合,且将直角三角尺绕点D按逆时针方向旋转.
(1)当直角三角尺的两直角边分别与矩形ABEF的两边BE、EF相交于点G、H时(如图11.1),求证:BG=EH.
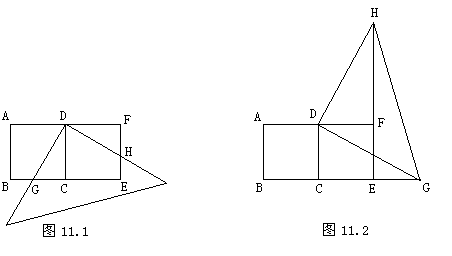 (2)当直角三角尺的两直角边分别与BE的延长线各EF的延长线相交于点G、H时(如图11.2),图11.1中的结论还成立吗?简要说明理由.
(2)当直角三角尺的两直角边分别与BE的延长线各EF的延长线相交于点G、H时(如图11.2),图11.1中的结论还成立吗?简要说明理由.
2006―2007学年度第一学期