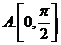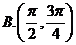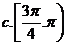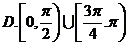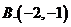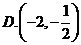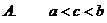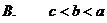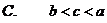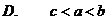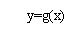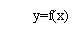1.已知: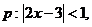

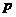 是
是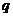 的( )
的( )
A.充分不必要条件 B。必要不充分条件 C.充要条件 D。既不充分也不必要条件
2.点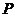 在曲线
在曲线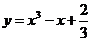 上移动,在点
上移动,在点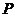 处的切线的倾斜角为
处的切线的倾斜角为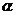 ,则
,则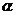 的取值范围是( )
的取值范围是( )
3.已知函数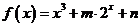 是奇函数,则( )
是奇函数,则( )
A. B。
B。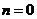 C。
C。 且
且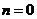 D。
D。 或
或
4.向量 ,若
,若 与
与 共线(其中
共线(其中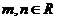 且
且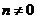 ),则
),则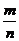 等于( )
等于( )
A.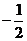 B。
B。 D。
D。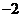
5.对于实数 ,符号
,符号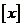 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如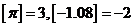 ,定义函数
,定义函数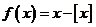 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A. B。方程
B。方程 有且仅有一个解
有且仅有一个解
C。函数 是周期函数
D。函数
是周期函数
D。函数 是增函数
是增函数
6.设 为椭圆
为椭圆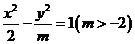 的离心率,且
的离心率,且 ,则实数
,则实数 的取值范围为( )
的取值范围为( )
7.已知 是定义在R上的周期为2的偶函数,当
是定义在R上的周期为2的偶函数,当 时,
时, 设
设 ,则
,则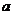 、
、 、
、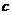 的大小关系为( )
的大小关系为( )
8.线段AB长为2,两个端点A、B分别在一个直二面角的两个面上,AB和两个面所成的角分别是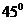 和
和 ,那么点A、B在这个二面角的棱上的射影C、D间的距离是( )
,那么点A、B在这个二面角的棱上的射影C、D间的距离是( )
A.1 B。 C。2 D。
C。2 D。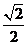
9.已知非零向量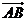 与
与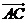 满足
满足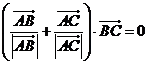 且
且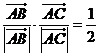 ,则
,则 为( )
为( )
A.三边均不相等的三角形 B。直角三角形
C.等腰非等边三角形 D。等边三角形

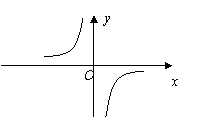 10.函数y=f(x)与y=g(x)的图象如下图:
10.函数y=f(x)与y=g(x)的图象如下图:
 则函数y=f(x)g(x)的图象可能为( )
则函数y=f(x)g(x)的图象可能为( )
A B C D
11..由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为( )
A. 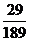 B.
B. 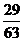 C.
C. 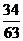 D.
D. 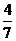
12.给出下列四个命题:
①若函数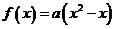 在区间
在区间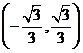 为减函数,则
为减函数,则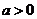 ;
;
②函数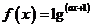 的定义域是
的定义域是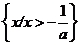 ;
;
③当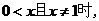
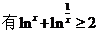 ;
;
④若M是圆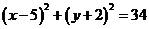 上的任意一点,
上的任意一点,
则点M关于 的对称点
的对称点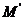 也在该圆上。
也在该圆上。
所有正确命题的序号是( )
A.①④ B。②④ C。①③ D。③④
第Ⅱ卷
注意事项:
请用黑色签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效。
本卷共10小题,共90分。
13.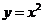 上一点
上一点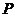 (非原点),在
(非原点),在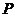 处引切线交
处引切线交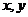 轴于
轴于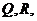 则
则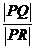 = 。
= 。
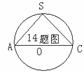 14.正四棱锥S―ABCD的5个顶点都在球O的表面上,过球心O的一个截面如图,棱锥的底面边长为1,则球心O到侧面SAB的距离为
。
14.正四棱锥S―ABCD的5个顶点都在球O的表面上,过球心O的一个截面如图,棱锥的底面边长为1,则球心O到侧面SAB的距离为
。
15.二项式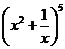 的展开式中
的展开式中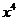 的系数为
。
的系数为
。
16.如果函数 的导函数的图象如右图所示,给出下列判断:
的导函数的图象如右图所示,给出下列判断:
①函数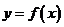 在区间
在区间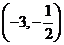 内单调递增;
内单调递增;
②函数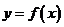 在区间
在区间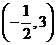 内单调递减;
内单调递减;
③函数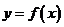 在区间
在区间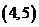 内单调递增;
内单调递增;
④当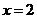 时,函数
时,函数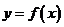 有极小值;
有极小值;
⑤当 时,函数
时,函数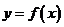 有极大值;
有极大值;
则上述判断中正确的是 。
(17)(本小题满分12分)求由正整数组成的集合S,使S中的元素之和等于元素之积。
(18)(本小题满分12分)已知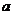 、
、 为非负数,
为非负数,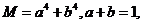 求
求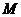 的最值。
的最值。
(19)(本小题满分12分)过正方体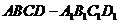 的8个顶点中任意两点的直线,与平面
的8个顶点中任意两点的直线,与平面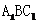 垂直的直线条数有多少?并加以证明。
垂直的直线条数有多少?并加以证明。
(20)。(本小题满分12分)湖南是劳务输出大省,据劳动村村长统计,第一季度,劳动村有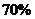 的农民在外打工,第二季度,劳动村有
的农民在外打工,第二季度,劳动村有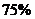 的农民在外打工,第三季度,劳动村有
的农民在外打工,第三季度,劳动村有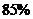 的农民在外打工,第四季度,劳动村有
的农民在外打工,第四季度,劳动村有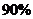 的农民在外打工,问劳动村至少有百分之几的农民全年在外打工?
的农民在外打工,问劳动村至少有百分之几的农民全年在外打工?
(21)、(本小题满分14分)两根等长的绳子挂一个物体,绳子受到的拉力大小为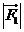 ,物体的重量为
,物体的重量为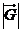 ,两绳子间的夹角为
,两绳子间的夹角为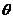 。
。
① 求绳子受到的拉力大小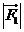 与两绳子间的夹角
与两绳子间的夹角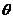 的关系;
的关系;
② 当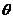 逐渐增大时,
逐渐增大时,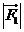 的大小怎样变化?
的大小怎样变化?
③ 当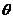 为何值时,
为何值时,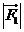 最小,最小值是多少?
最小,最小值是多少?
④当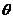 为何值时,
为何值时,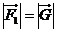 ?
?
(22)、(本小题满分12分)给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点。
(Ⅰ)设l的斜率为1,求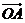 与
与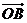 的夹角的大小;
的夹角的大小;
(Ⅱ)设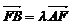 ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
湖南省衡阳市祁东县育贤中学高三文科数学试题(2007年2月)