1.复数z= 的值为(    )

A. (1＋i)   B. －(1＋i)  C. (1－i)    D. －(1－i)

2.在等比数列{a_n}中, a₃= , S₃=   , 则首项a₁=(   )

A.    B. －   C. 6或－    D. 6或

3.已知角α的正切线是单位长度的有向线段,那么角α的终边在(  )

A. x轴上   B. y轴上  C.直线y=x上   D.直线y=x 或y=－x上

4.已知全集U=R, A= {x| ≥0}, 则C_uA=(   )

A.{x|－1<x≤0}   B. {x|－1<x<0}   C. {x|－1≤x<0}    D. {x|－1≤x≤0}

5.在正方体ABCD－A₁B₁C₁D₁中, E、F、M分别为AA₁,C₁D₁,BC的中点,那么直线B₁E与FM所成角的余弦值为(   )

A.0   B.1  C.       D.

6.若AB过椭圆 ＋ =1 中心的弦, F₁为椭圆的焦点, 则△F₁AB面积的最大值为(    )

A. 6   B.12   C.24   D.48

7.在△ABC中, D为AC边的中点, E为AB上一点, BC、CF交于一点F, 且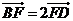 , 若, 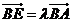, 则实数λ的值为(    )

A.      B.     C.     D.

8.将4个相同的小球投入3个不同的盒内, 不同的投入方式共有(  )

A. 4³种    B. 3⁴种    C. 15种    D. 30种

9.如果实数x、y满足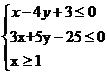, 目标函数z=kx＋y的最大值为12, 最小值3, 那么实数k的值为(    )

A. 2  B. －2   C.    D.不存在

10. 函数y=|cos2x|＋|cosx|的值域为(   )

A. [, 2]    B. [,2]    C. [, ]  D.[,2]                        

二.填空题：本大题共5小题，每小题5分，共25分.

11.(1＋x)⁶(1－x) 展开式中x²项的系数是________

12. x→1lim= _________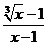

13.如果直线l 过定点M(1,2)且与抛物线y=2x²有且仅有一个公共点, 那么直线l的方程为_______

14.正四棱锥S－ABCD内接于一个半径为R的球, 那么这个正四棱锥体积的最大值为_____

15. 函数f(x)=x³－3x²＋6x－7的图象是中心对称图形, 其对称中心的坐标为_________

三.解答题：本大题共6小题，共75分.解答应写了文字说明，证明过程或演算步骤.

16.(本小题满分12分)

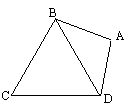如图, 在平面四边形ABCD中, AB=AD=1, ∠BAD=θ, 而△BCD是正三角形,

(1) 将四边形ABCD面积S表示为θ的函数;

(2) 求S的最大值及此时θ角的值.

17. (本小题满分12分)

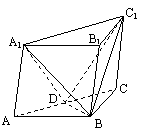如图, 在斜三棱柱ABC－A₁B₁C₁中 AB=BC=2, ∠ABC= 120°, 又顶点A₁在底面ABC上的射影落在AC上, 侧棱AA₁与底面成60°的角, D为AC的中点.

(1) 求证: AA₁⊥BD;

(2)若面A₁DB⊥面DC₁B, 求侧棱AA₁之长.

18. (本小题满分12分)

A袋中装有大小相同的红球1个, 白球2个, B袋中装有与A袋中相同大小的红球2个, 白球3个. 先从A中取出1个球投入B中, 然后从B中取出2个球. 设ξ表示从B中取出红球的个数.

(1) 求ξ=2时的概率;

(2)求ξ的分布列和数学期望

19. (本小题满分13分)

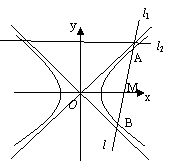如图, 直线l : y= (x－2) 和双曲线C: － = 1 (a>0,b>0) 交于A、B两点, |AB|= , 又l关于直线l₁: y= x对称的直线l₂与x轴平行.

(1)求双曲线C的离心率；

(2)求双曲线C的方程.

20. (本小题满分13分)

已知数列{a_n}的前n项之和S_n与a_n满足关系式: nS_n＋1=(n＋2)S_n＋a_n＋2 (n∈N_＋)

(1)若a₁=0 , 求a₂,a₃的值;

(2) 求证: a₁=0是数列{a_n}为等差数列的充要条件.

21. (本小题满分13分)

已知函数f(x)=x²＋2x＋alnx

(1)若函数f(x)在区间(0,1)上恒为单调函数, 求实数a的取值范围;

(2) 当t≥1时, 不等式f(2t－1) ≥2f(t)－3恒成立, 求实数a的取值范围.