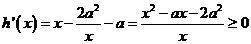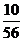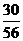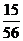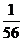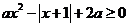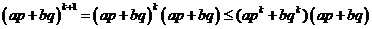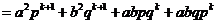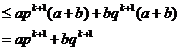1、已知集合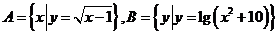 ,则有( )
,则有( )
(A)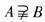 (B)
(B)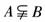 (C)
(C) (D)A=CRB
(D)A=CRB
2、如果复数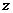 满足:
满足: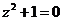 ,则
,则 (
(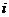 为虚数单位)的值为( )
为虚数单位)的值为( )
(A)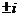 (B)
(B)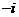 (C)
(C)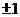 (D)1
(D)1
3、已知随机变量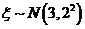 ,若
,若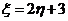 ,则
,则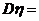 ( )
( )
(A)0 (B)1 (C)2 (D)4
4、已知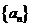 是正项的等差数列,如果满足:
是正项的等差数列,如果满足: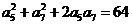 ,则数列
,则数列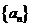 的前11项的和为( )
的前11项的和为( )
(A)8 (B)44 (C)56 (D)64
5、函数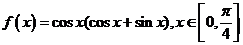 的值域是( )
的值域是( )
(A)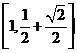 (B)
(B)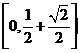 (C)
(C)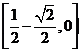 (D)
(D)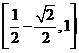
6、设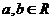 ,则“
,则“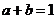 ”是“
”是“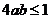 ”的( )条件
”的( )条件
(A)充分非必要 (B)必要非充分 (C)充分必要 (D)既不充分也不必要
7、函数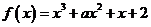 在
在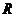 上存在极值点,则实数
上存在极值点,则实数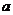 的取值范围是( )
的取值范围是( )
(A)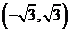 (B)
(B)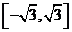
(C)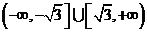 (D)
(D)
8、同时抛掷三枚骰子,出现正面朝上的点数之和不大于5的概率是( )
(A)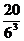 (B)
(B)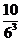 (C)
(C)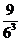 (D)
(D)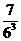
9、已知平面向量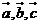 满足
满足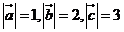 ,且向量
,且向量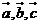 两两所成的角相等,则
两两所成的角相等,则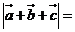 ( )
( )
(A)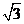 (B)
(B) 或
或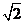 (C)6
(D)
(C)6
(D) 或
或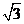
10、设二次函数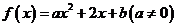 ,若方程
,若方程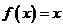 无实数解,则方程
无实数解,则方程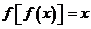 的实数根的个数为( )
的实数根的个数为( )
(A)0 (B)2 (C)4 (D)4个以上
第Ⅱ卷(非选择题,共100分)
11、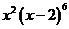 展开式中
展开式中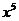 的系数是 ▲ .
的系数是 ▲ .
12、用0,1,2,3,4这五个数字组成无重复数字的五位数,其中恰有一个偶数夹在两个奇数之间的五位数的个数是 ▲ (用数字作答).
13、在直角三角形ABC中,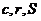 分别表示它的斜边、内切圆半径和面积,则
分别表示它的斜边、内切圆半径和面积,则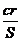 的最小值是 ▲ .
的最小值是 ▲ .
14、命题:①若函数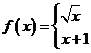
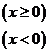 ,则
,则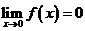 ;②若
;②若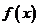 在
在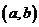 内连续,则
内连续,则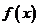 在
在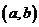 内一定存在最大值和最小值;③已知
内一定存在最大值和最小值;③已知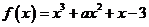 ,若
,若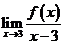 存在,则
存在,则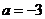 ;④
;④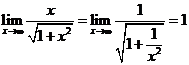 .则其中不正确的命题的序号是
▲ .
.则其中不正确的命题的序号是
▲ .
15.(本小题满分14分)已知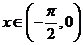 ,
,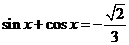 .
.
(1)求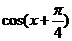 的值;
的值;
(2)求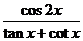 的值.
的值.
16.(本小题满分14分)已知函数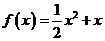 ,
,
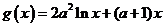 .
.
(1)求过点 与曲线
与曲线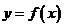 相切的切线方程;
相切的切线方程;
(2)如果函数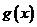 在定义域内存在导数为零的点,求实数
在定义域内存在导数为零的点,求实数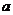 的取值范围;
的取值范围;
(3)设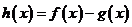 ,求函数
,求函数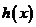 的单调递增区间.
的单调递增区间.
17.(本小题满分14分)
在一袋中有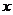 个红球、3个黑球和2个白球,现从中任取3个.
个红球、3个黑球和2个白球,现从中任取3个.
(1)如果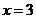 ,求取出的3球中颜色都相同的概率;
,求取出的3球中颜色都相同的概率;
(2)在(1)的前提下,设 表示取出的3球中红球的个数,求
表示取出的3球中红球的个数,求 的概率分布及数学期望
的概率分布及数学期望
(3)如果取出的3球的颜色各不相同的概率为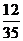 ,求
,求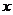 的值.
的值.
18.(本小题满分14分)已知正项数列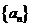 满足:
满足:
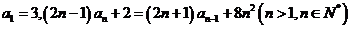 .
.
(1)求证:数列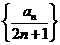 是等差数列;
是等差数列;
(2)求数列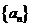 的通项
的通项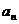 ;
;
(3)求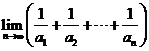 的值.
的值.
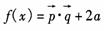 19.(本小题满分14分)已知向量
19.(本小题满分14分)已知向量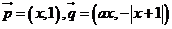 ,设
,设
(1)若 ,求证:函数
,求证:函数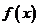 的值恒正;
的值恒正;
(2)如果不等式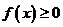 对一切实数
对一切实数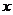 恒成立,求实数
恒成立,求实数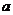 的取值范围.
的取值范围.
20.(本小题满分14分)设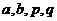 都是正实数,且
都是正实数,且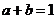 ,定义函数
,定义函数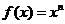
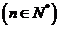 .
.
(1)试比较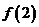 与
与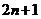 的大小;
的大小;
(2)证明: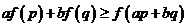 .
.
2006学年浙江省五校联考(一)
数学(理科)答题卷
试题
一
二
三
总分
15
16
17
18
19
20
得分
卷Ⅰ(选择题,共50分)
题目
1
2
3
4
5
6
7
8
9
10
卷Ⅱ(非选择题,共100分)
11. 12.
13. 14.
15.(本小题满分14分)已知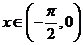 ,
,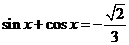 .
.
(1)求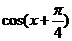 的值;
的值;
(2)求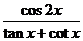 的值.
的值.
16.(本小题满分14分)已知函数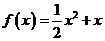 ,
,
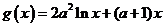 .
.
(1)求过点 与曲线
与曲线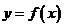 相切的切线方程;
相切的切线方程;
(2)如果函数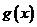 在定义域内存在导数为零的点,求实数
在定义域内存在导数为零的点,求实数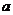 的取值范围;
的取值范围;
(3)设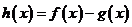 ,求函数
,求函数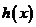 的单调递增区间
的单调递增区间
17.(本小题满分14分)
在一袋中有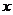 个红球、3个黑球和2个白球,现从中任取3个.
个红球、3个黑球和2个白球,现从中任取3个.
(1)如果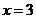 ,求取出的3球中颜色都相同的概率;
,求取出的3球中颜色都相同的概率;
(2)在(1)的前提下,设 表示取出的3球中红球的个数,求
表示取出的3球中红球的个数,求 的概率分布及数学期望
的概率分布及数学期望
(3)如果取出的3球的颜色各不相同的概率为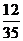 ,求
,求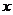 的值.
的值.
18.(本小题满分14分)已知正项数列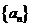 满足:
满足:
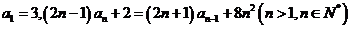 .
.
(1)求证:数列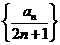 是等差数列;
是等差数列;
(2)求数列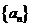 的通项
的通项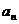 ;
;
(3)求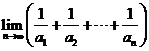 的值.
的值.
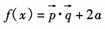 19.(本小题满分14分)已知向量
19.(本小题满分14分)已知向量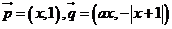 ,设(1)若
,设(1)若 ,求证:函数
,求证:函数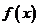 的值恒正;
的值恒正;
(2)如果不等式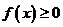 对一切实数
对一切实数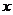 恒成立,求实数
恒成立,求实数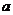 的取值范围.
的取值范围.
20.(本小题满分14分)设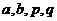 都是正实数,且
都是正实数,且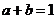 ,定义函数
,定义函数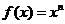
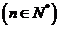 .
.
(1)试比较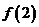 与
与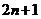 的大小;
的大小;
(2)证明: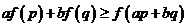 .
.
浙江省2006学年高三五校联考数学卷(理科)评分参考
题号
1
2
3
4
5
6
7
8
9
10
答案
C
C
B
B
A
A
D
B
D
A
11. 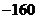 12.28 13.
12.28 13.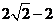 14.①②④
14.①②④
15.(1)∵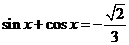 ,∴
,∴ 2分
2分
∵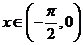 ,∴
,∴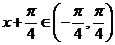 ,
4分
,
4分
∴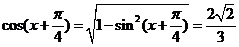 .
.
(2)∵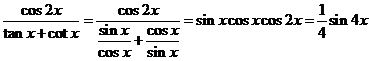 8分
8分
又∵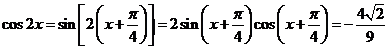 10分
10分
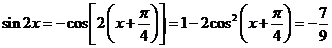 12分
12分
∴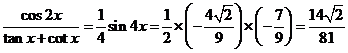 14分
14分
16.(1) ,∵点
,∵点 在曲线上,∴
在曲线上,∴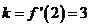
∴所求的切线方程为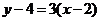 ,即
,即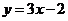 3分
3分
(2)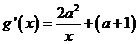
若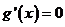 ,则
,则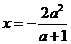 .
.
∵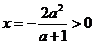 ,∴
,∴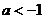 .
6分
.
6分
(3)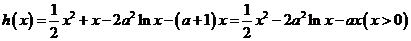
即 11分
11分
当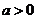 时,单调递增区间为
时,单调递增区间为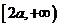
当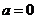 时,单调递增区间为
时,单调递增区间为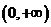
当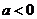 时,单调递增区间为
时,单调递增区间为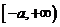 14分
14分
17.(1)设3球中颜色都相同的事件为A
当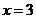 时,
时,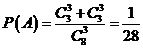 4分
4分
(2)

0
1
2
3
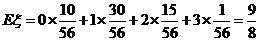 9分
9分
(3)设取出3球中颜色都不相同的事件为B,则有
 11分
11分
依题意有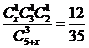
化简得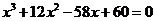 12分
12分
即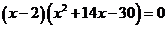
因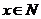 ,所以
,所以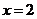 14分
14分
18.(1)∵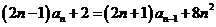
∴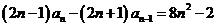
即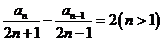 4分
4分
∵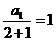 ,∴
,∴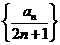 是以1为首项,2为公差的等差数列 5分
是以1为首项,2为公差的等差数列 5分
(2)∵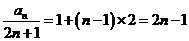
∴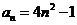 9分
9分
(3)∵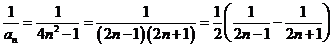 11分
11分
∴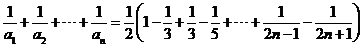 12分
12分
∴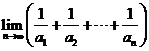
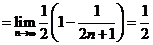 14分
14分
19.(1)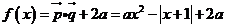 1分
1分
∵ ,∴
,∴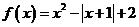
当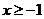 时,
时,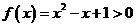 恒成立
3分
恒成立
3分
当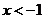 时,
时,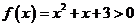 恒成立
5分
恒成立
5分
∴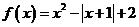 对一切
对一切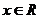 都恒正.
6分
都恒正.
6分
(2)方法1:因为对一切实数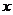 ,都有
,都有
即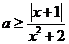 8分
8分
设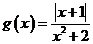 ,则
,则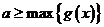 9分
9分
令 ,则
,则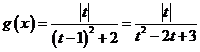
(?)当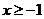 ,即
,即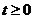 时,有
时,有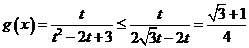
当且仅当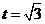 ,即
,即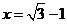 时,等号成立.
11分
时,等号成立.
11分
(?)当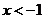 ,即
,即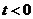 时,有
时,有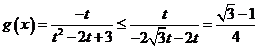
当且仅当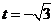 ,即
,即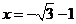 时,等号成立.
13分
时,等号成立.
13分
综合可得 ,所以实数
,所以实数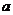 的取值范围是
的取值范围是 14分
14分
方法2:把问题转化为不等式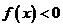 的解集为空集
的解集为空集
即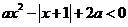 7分
7分
当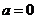 ,则
,则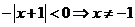 ,矛盾
8分
,矛盾
8分
当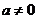 时,不等式
时,不等式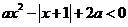 要无解
要无解
(?)当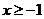 时,
时,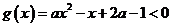 无解
无解
若 时,则
时,则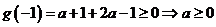 矛盾
矛盾
若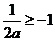 时,则
时,则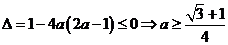 或
或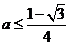
则有 (1)
11分
(1)
11分
(?)当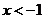 ,
,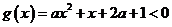 无解
无解
若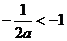 时,
时,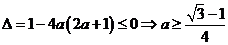 或
或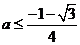
则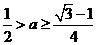
若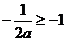 时,则
时,则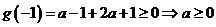
则
综合有 (2)
13分
(2)
13分
所以实数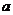 的取值范围是
的取值范围是 14分
14分
20.(1)当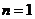 时,
时,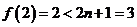 1分
1分
当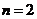 时,
时,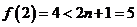 2分
2分
当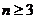 时,
时,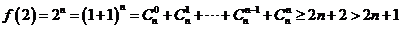
(用数学归纳法也可以证明). 6分
(2)即证: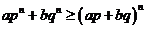 7分
7分
证法1:(数学归纳法)
(?)当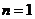 时,
时,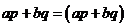 不等式成立,
8分
不等式成立,
8分
(?)假设 时,有
时,有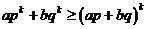
当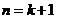 时,
时,
因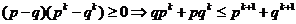
故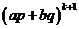
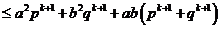
即当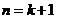 时命题成立.
13分
时命题成立.
13分
根据(?)(?)可得对一切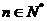 不等式均成立.
14分
不等式均成立.
14分
方法2:构造函数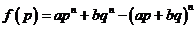
若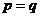 ,则等号成立,
7分
,则等号成立,
7分
若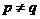 ,根据对称性,不妨设
,根据对称性,不妨设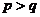 ,当
,当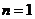 时,不等式成立,
8分
时,不等式成立,
8分
当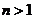 时,
时,
因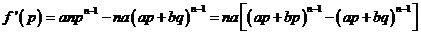 10分
10分
∵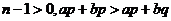
∴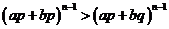
∴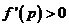 ,即
,即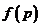 在
在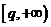 上是单调增函数
12分
上是单调增函数
12分
当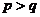 时,有
时,有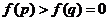
∴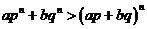
综上得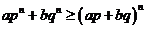 即
即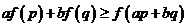 .
14分
.
14分