1.函数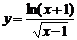 的定义域是( )
的定义域是( )
A.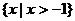 B.
B.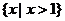 C.
C.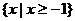 D.
D.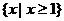
2.已知全集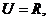 集合
集合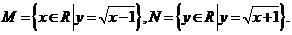 则
则 是( )
是( )
A.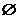 B.
B.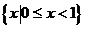 C.
C.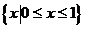 D.
D. 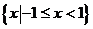
3.在等差数列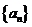 中,已知
中,已知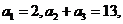 则
则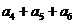 等于 ( )
等于 ( )
A.40 B
4.函数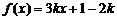 在(-1,1)上存在
在(-1,1)上存在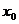 ,使
,使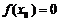 ,则
,则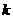 的取值范围是( )
的取值范围是( )
A.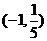 B.
B.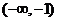 C.
C.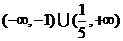 D.
D.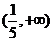
5.已知数集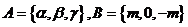 ,
,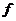 是从
是从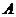 到
到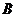 的映射, 则满足
的映射, 则满足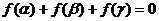 的映射共有 ( )
的映射共有 ( )
A.6个 B.7个 C.9个 D.27个
6.过曲线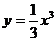 上点
上点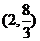 的切线方程是 ( )
的切线方程是 ( )
A.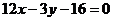 B.
B.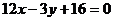 C.
C.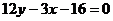 D.
D.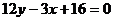
7.在等比数列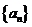 中,
中,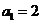 ,前
,前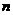 项和为
项和为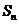 ,若数列
,若数列 也是等比数列,则
也是等比数列,则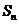 等于( )
等于( )
A.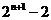 B.
B. 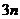 C.
C. 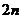 D.
D.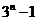
8. 已知函数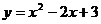 在区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
在区间[0,m]上有最大值3,最小值2,则m的取值范围是( )
 A.
A.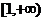 B.[0,2] C.
B.[0,2] C.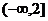 D.[1,2]
D.[1,2]
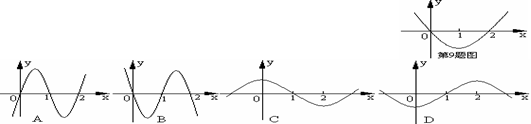
9. 设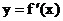 是函数
是函数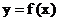 的导数,
的导数, 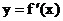 的图象如图所示,
的图象如图所示,
则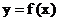 的图象最有可能是 ( )
的图象最有可能是 ( )
10.设Sn是等差数列{an}的前n项和,若 =,则 = ( )
A. B. C. D.
11.函数y=log x在
x在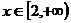 上总有|y|>1,则a的取值范围是( )
上总有|y|>1,则a的取值范围是( )
A. 或
或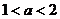 B.
B.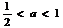 或
或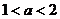
C. 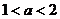 D.
D. 或
或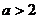
12.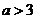 ,则方程
,则方程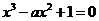 在(0,2)上恰好有 ( )
在(0,2)上恰好有 ( )
A. 0 个根 B. 1个根 C.2个根 D. 3个根
13.已知等差数列共有10项,其中奇数项之和15,偶数项之和为30,则其公差是
14.已知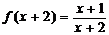 ,则
,则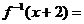
15在数列{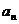 }中,若
}中,若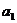 =1,
=1, 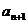 =2
=2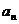 +3 (n≥1),则该数列的通项
+3 (n≥1),则该数列的通项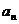 =__ ___.
=__ ___.
16.设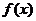 是R上以2为周期的奇函数,已知当
是R上以2为周期的奇函数,已知当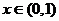 时,
时,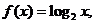 那么
那么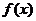 在
在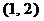 上的解析式是
上的解析式是
17. 已知全集为R,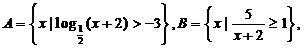 求
求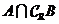
18.已知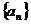 是等比数列,
是等比数列,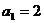 ,
,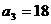 ;
;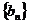 是等差数列,
是等差数列,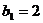 ,
, .
.
(1)求数列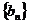 的通项公式;
的通项公式;
(2)求数列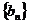 的前
的前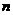 项和
项和 的公式
的公式
19.已知函数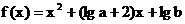 满足
满足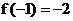 且对于任意
且对于任意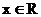 , 恒有
, 恒有
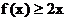 成立.
成立.
(1) 求实数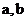 的值;
的值;
(2) 解不等式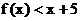 .
.
20.数列{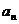 }的前n项和记为
}的前n项和记为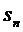 ,已知
,已知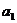 =1,
=1,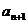 =
=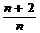
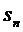 (n=1,2,3,…)
(n=1,2,3,…)
证明:(Ⅰ)数列{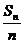 }是等比数列;(Ⅱ)
}是等比数列;(Ⅱ)  =4
=4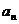
21、已知函数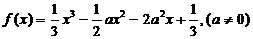 .
.
(1) 若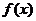 在区间
在区间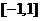 上是减函数, 求实数
上是减函数, 求实数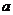 的取值范围;
的取值范围;
(2) 若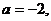 求
求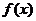 在区间
在区间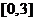 上的最大值和最小值.
上的最大值和最小值.
22.设函数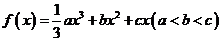 ,其图象在点
,其图象在点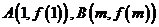 处的切线的斜率分别为0,-a.
处的切线的斜率分别为0,-a.
(1)求证: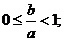
(2)若函数f(x)的递增区间为[s,t],求|s-t|的取值范围;
(3)若当

