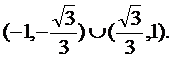(3)已知向量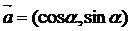 ,向量
,向量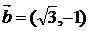 ,则
,则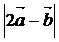 的最大值是
的最大值是
A.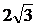 B.4
C.12
D.1
B.4
C.12
D.1
本小题主要考查向量与三角结合的基本运算,考察运算能力。试题给出两个向量的坐标,要求考生会利用向量的坐标运算、三角函数的恒等变换,用多种方法确定向量的模的最大值.考察的重点是学生对向量的概念、向量的运算、向量的模的性质的理解与应用,方法较多,考查较灵活.
解法1: ∵
∵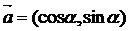 ,
,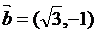 ,
,
解法2: ∵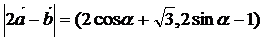
∴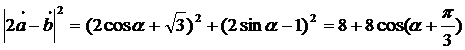
∴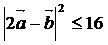 ,
,
∴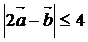 .
.
4.在 这四个函数中,当
这四个函数中,当 时,使
时,使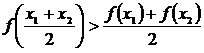 恒成立的函数的个数是
恒成立的函数的个数是
A.0 B.1 C.2 D.3
本小题主要考查函数的凹凸性,试题给出了四个基本初等函数,要求考生根据函数的图像研究函数的性质---凹凸性,对试题中的不等关系式: ,既可以利用函数的图像直观的认识,也可以通过代数式的不等关系来理解。考查的重点是结合函数的图像准确理解凹凸的含义.
,既可以利用函数的图像直观的认识,也可以通过代数式的不等关系来理解。考查的重点是结合函数的图像准确理解凹凸的含义.
解答:B
2.填空题
(1)已知实数 满足等式
满足等式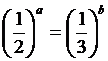 ,写出
,写出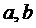 满足条件的一个关系式 .(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
满足条件的一个关系式 .(注:填上你认为可以成为真命题的一种情形即可,不必考虑所有可能的情形)
本小题主要考查指数式、指对互化以及分类讨论数学思想方法.此题是一个开放性问题,该类问题有助于考察学生的发散思维和创造意识.
解答:①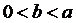 ②
②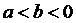 ③
③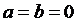 ,等.
,等.
(2)求满足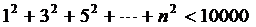 的最大整数解的程序框图A处应为
.
的最大整数解的程序框图A处应为
.
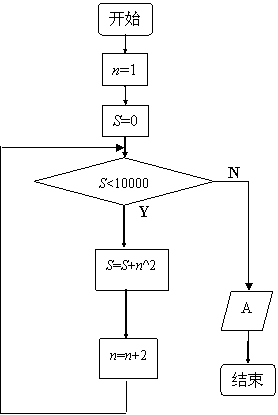 |
本小题主要考查程序框图的知识和分析问题、解决问题的逻辑思维能力,试题给出了满足题目条件的框图,在给定框图结构的前提条件下,要求考生会读框图、理解框图,并根据流程,写出最后输出框中的内容.考查的重点是学生对程序框图的认识,利用框图流程,不难写出最后的输出结果.该题所涉及内容为新课程新增内容,体现了数学课程与时俱进,反映了计算机科学发展对数学课程的影响,关注此类问题既考察学生对算法思想的了解和掌握,同时还有助于培养学生学习科学技术的兴趣.
解答: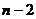
(3)已知两个圆: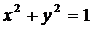 ①与
①与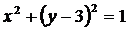 ②,则由①式减去②式可得上述两圆的对称轴方程,将上述命题在曲线仍为圆
②,则由①式减去②式可得上述两圆的对称轴方程,将上述命题在曲线仍为圆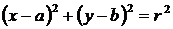 和
和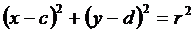 的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例,推广的命题为 .
的情况下加以推广,即要求得到一个更一般的命题,而已知命题应成为所推广命题的一个特例,推广的命题为 .
本小题主要考查圆的方程、圆的公共弦方程的概念,考查抽象思维能力和归纳推广的能力.
解答: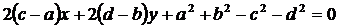
(4)已知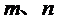 是不同的直线,
是不同的直线,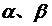 是不重合的平面,给出下列命题:
是不重合的平面,给出下列命题:
①若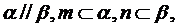 则
则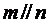 ;
;
②若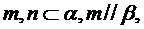 则
则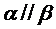 ;
;
③若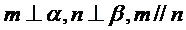 ,则
,则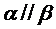 ;
;
④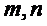 是两条异面直线,若
是两条异面直线,若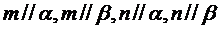 ,则
,则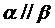 .
.
上面的命题中,真命题的序号是 (写出所有真命题的序号).
(写出所有真命题的序号).
本小题主要考查直线与直线、直线与平面、平面与平面的位置关系,考查逻辑推理和空间想象能力.
解答:③④
3.解答题
(1)已知函数 ,证明:
,证明:
①经过这个函数图象上任意两个不同的点的直线不平行与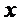 轴;②这个函数的图象关于直线
轴;②这个函数的图象关于直线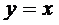 成轴对称图形.
成轴对称图形.
本小题主要考查函数图象的性质、平行直线和对称图形以及推理论证能力.
证明:①设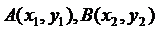 是函数图象上任意不同的两个点,则
是函数图象上任意不同的两个点,则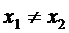 ,且
,且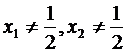
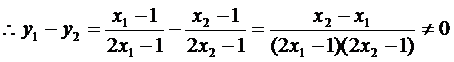 .
.
即 ,所以直线
,所以直线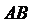 不平行于
不平行于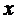 轴.
轴.
②设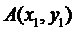 是函数图象上的任意一个点,则
是函数图象上的任意一个点,则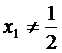 ,
,
且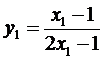 .
…………(*)
.
…………(*)
所以,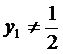 ,否则有
,否则有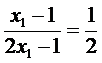 ,得
,得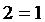 ,这是不可能的.因此
,这是不可能的.因此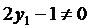 ;由(*)式得:
;由(*)式得:
此式表示:点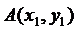 关于直线
关于直线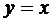 的对称点
的对称点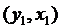 在函数图象上,由于
在函数图象上,由于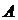 的任意性,知函数的图象关于直线
的任意性,知函数的图象关于直线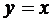 成轴对称图形.
成轴对称图形.
(2)有一批影碟机(VCD)原价为每台800元,在甲乙两家家电商场均有销售.甲商场用如下的方法促销:买一台单价为780元,买两台每台单价都为760元,依次类推,每多一台则所买各台单价均再减少20元,但每台最低不能低于440元;乙商场一律都按原价的75%销售.某单位需购买一批此类影碟机,问去哪家商场购买花费较少?
本小题是实际问题,考查的目标是要求考生应用数学知识作出分析,给出合理的判断,考查学生应用数学知识分析问题和解决问题的能力,本题的实际背景是商品销售问题,对考生比较公平,与生活相关性也比较高.本题考查的知识点是分段函数和不等式.
解:设某单位需要购买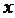 台影碟机,甲乙两商场的购货款的差价为
台影碟机,甲乙两商场的购货款的差价为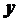 ,
,
则因为去甲商场购买共花费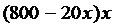 ,据题意,
,据题意,
去乙商场购买共花费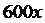 ,
,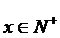 .
.
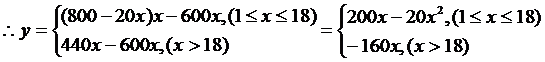 得
得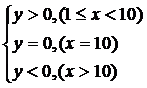
故若买少于10台,去乙商场购买花费较少; 若买10台,去甲、乙商场购买花费一样;若买超过10台,去甲商场购买花费较少.
(3)某地现有耕地10000公顷,规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?
(粮食单产=总产量/耕地面积,人均粮食占有量=总产量/总人口数)
本小题的背景是人口增长和耕地流失的控制问题,这是当前国情教育中的一个十分突出的问题.通过解决此类问题有助于增强学生的社会责任感和土地保护意识。该题考查的是数列知识,还把利用二项式定理进行近似计算的考查揉合其中,比较新颖.
解:设耕地平均每年至多减少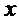 公顷,现有人口
公顷,现有人口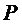 人,粮食单产
人,粮食单产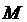 吨/公顷,依题意得:
吨/公顷,依题意得:
得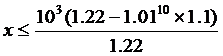
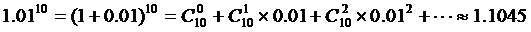 所以
所以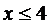
答:耕地平均每年至多减少4公顷.
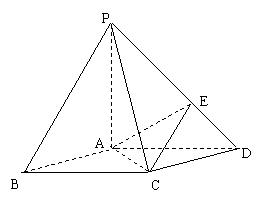
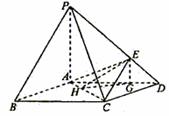
(4)如图,在底面是菱形的四棱锥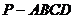 中,
中,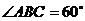 ,
, ,
,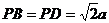 ,点
,点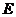 在
在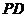 上,且
上,且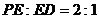 .
.
(I)证明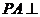 平面
平面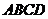 ;
;
(II)求以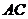 为棱,
为棱,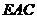 与
与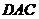 为面的二面角
为面的二面角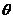 的大小;
的大小;
 (Ⅲ)在棱
(Ⅲ)在棱 上是否存在一点
上是否存在一点 ,使
,使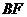
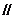 平面
平面 ?证明你的结论.
?证明你的结论.
本小题主要考查了棱锥、直线与平面垂直的判定与性质,二面角及二面角的平面角、直线与平面平行的判定和性质,同时考查了利用空间向量解决立体几何问题的转换能力、一定的计算能力以及逻辑推理能力.
第3问在设问上有一定开放性,这对空间观念的要求,对空间图形转换要求,在水平层次上就有较大的提高,切入点是从特殊点开始进行探究.
此题可用空间向量法解决,关键是能合理的构建空间坐标系.
总之,本题在解决方法上利用向量手段解决几何问题,很好地体现了数学的和谐美。同时,空间向量在立体几何中的应用为考生创造了几何证明的新思路,体现了解决问题策略的多样化。另外,本题通过开放性问题的设计,给学生留出了较大的思维空间,为学生灵活运用所学知识解决问题建立了一个平台.
|

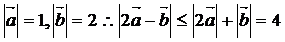
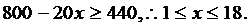
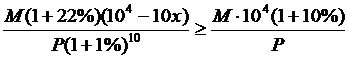
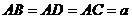 ,
, 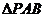 中,由
中,由 知
知 .
.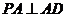 ,所以
,所以
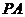 交
交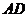 于
于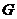 ,
,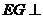 平面
平面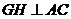 于
于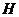 ,连结
,连结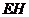 ,
,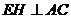 ,
,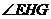 即为二面角
即为二面角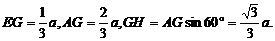

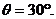

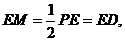 知
知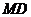 的中点.
的中点.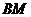 、
、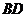 ,设
,设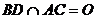 ,
,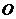 为
为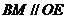 . ②
. ②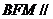 平面
平面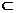 平面
平面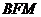 ,所以
,所以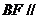 平面
平面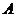 为坐标原点,直线
为坐标原点,直线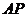 分别为
分别为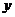 轴、
轴、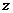 轴,过
轴,过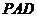 的直线为
的直线为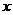 轴,建立空间直角坐标系如图.由题设条件,相关各点的坐标分别为
轴,建立空间直角坐标系如图.由题设条件,相关各点的坐标分别为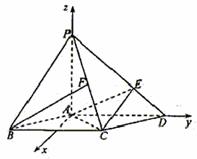
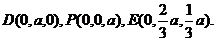
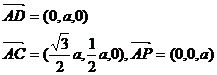
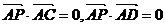
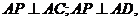 又
又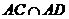 于
于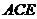 的发向量为
的发向量为
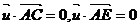 得
得 又平面
又平面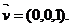
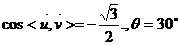

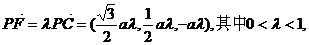 则
则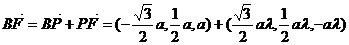
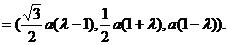 令
令  得
得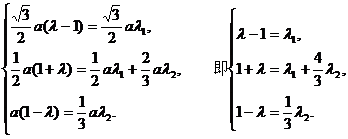
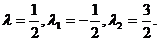 即
即 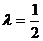 时,
时,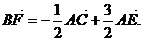
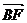 、
、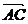 、
、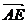 共面.
共面. 平面
平面
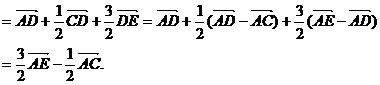
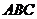 ,从而
,从而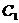 的方程为
的方程为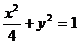 ,
,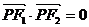 的的点
的的点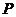 的轨迹方程
的轨迹方程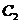 ;
;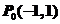 作弦
作弦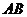 ,当弦
,当弦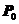 平分时,求直线
平分时,求直线 的左、右焦点分别为
的左、右焦点分别为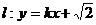 与双曲线
与双曲线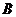 ,且
,且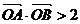 (其中
(其中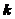 的取值范围.
的取值范围.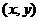 ,由椭圆的方程可知
,由椭圆的方程可知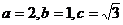
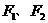 的坐标分别为(-
的坐标分别为(-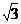 ,
,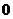 )、(
)、(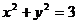
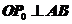 ,直线
,直线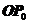 的斜率为-1,
的斜率为-1,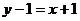 ,
,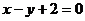
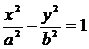 ,则
,则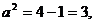 再由
再由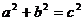 得
得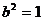 .
.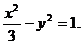

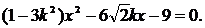
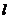 与双曲线交于不同的两点得
与双曲线交于不同的两点得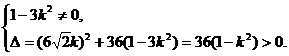
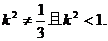 ① 设
① 设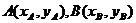 ,则
,则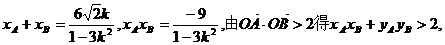
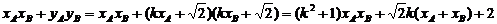

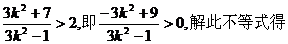
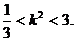 ②
②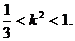
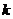 的取值范围为
的取值范围为