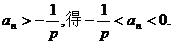1. 已知数列 的前n项和
的前n项和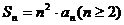 ,而
,而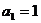 ,通过计算
,通过计算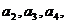 猜想
猜想
( )
A.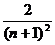 B.
B.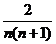 C.
C.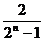 D.
D.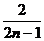
2.已知数列 的通项公式
的通项公式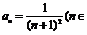 N*),记
N*),记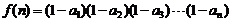 ,
,
通过计算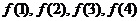 的值,由此猜想
的值,由此猜想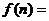 ( )
( )
A.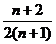 B.
B.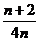 C.
C.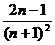 D.
D.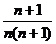
3.数列 中,a1=1,Sn表示前n项和,且Sn,Sn+1,2S1成等差数列,通过计算S1,S2,
中,a1=1,Sn表示前n项和,且Sn,Sn+1,2S1成等差数列,通过计算S1,S2,
S3,猜想Sn= ( )
A.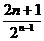 B.
B.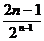 C.
C.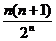 D.1-
D.1-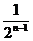
4.已知a1=1,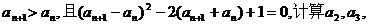 然后猜想
然后猜想
( )
A.n B.n2 C.n3 D.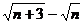
5.设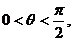 已知
已知 则猜想
则猜想 ( )
( )
A.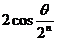 B.
B.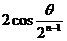 C.
C.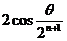 D.
D.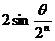
6.从一楼到二楼的楼梯共有n级台阶,每步只能跨上1级或2级,走完这n级台阶共有
种走法,则下面的猜想正确的是 ( )
A.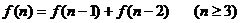 B.
B.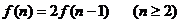
C.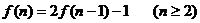 D.
D.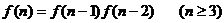
7.已知数列 中,
中, 通过计算
通过计算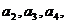 然后猜想
然后猜想
8.在数列 中,
中,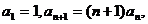 通过计算
通过计算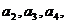 然后猜想
然后猜想
9.设数列 的前n项和为Sn,已知Sn=2n-an(n∈N+),通过计算数列的前四项,猜想
的前n项和为Sn,已知Sn=2n-an(n∈N+),通过计算数列的前四项,猜想
10.已知函数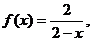 记数列
记数列 的前n项和为Sn,且
的前n项和为Sn,且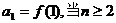 时,
时,
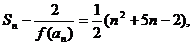 则通过计算
则通过计算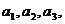 的值,猜想
的值,猜想 的通项公式
的通项公式
11.是否存在常数a,b,c,使等式
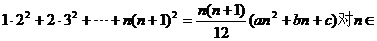 N+都成立,并证明你的结论.
N+都成立,并证明你的结论.
12.已知数列 的各项为正数,其前n项和为Sn,又
的各项为正数,其前n项和为Sn,又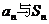 满足关系式:
满足关系式:
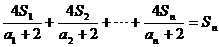 ,试求
,试求 的通项公式.
的通项公式.
13.已知数列 的各项为正数,Sn为前n项和,且
的各项为正数,Sn为前n项和,且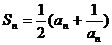 ,归纳出an的公式,并证明你的结论.
,归纳出an的公式,并证明你的结论.
14.已知数列 是等差数列,
是等差数列,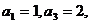 设
设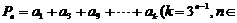 N+),
N+),
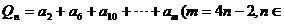 N+),问Pn与Qn哪一个大?证明你的结论.
N+),问Pn与Qn哪一个大?证明你的结论.
15.已知数列 :
: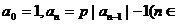 N*
N* 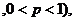
(Ⅰ)归纳出an的公式,并证明你的结论;
(Ⅱ)求证:
答案与解析
一、1.B 2.A 3.D 4.B 5.B 6.A
二、7.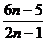 8.n! 9.
8.n! 9.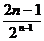 10.n+1
10.n+1
11.令n=1得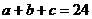 ①, 令n=2得
①, 令n=2得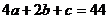 ②,
②,
令n=3得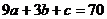 ③, 解①、②、③得a=3,b=11,c=10,记原式的左边为Sn,用数学归纳法证明猜想
③, 解①、②、③得a=3,b=11,c=10,记原式的左边为Sn,用数学归纳法证明猜想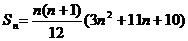 (证明略)
(证明略)
12.计算得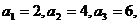 猜测
猜测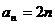 ,用数学归纳法证明(证明略).
,用数学归纳法证明(证明略).
13.∵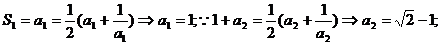
∵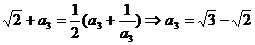 ,…,猜想
,…,猜想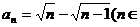 N*).用数学归纳法证明(略).
N*).用数学归纳法证明(略).
14.∵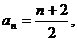 ∴
∴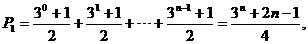
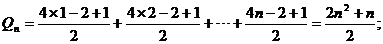 计算得①
计算得①
当1≤n≤3时,Pn<Qn;②猜想n≥4时Pn>Qn,用数学归纳法证明,即证:当n≥4时
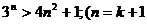 时用比较法证)
时用比较法证)
15.(Ⅰ)∵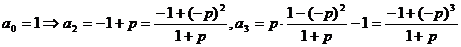 ,…,猜测
,…,猜测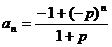 ,数学归纳法证明(略).
,数学归纳法证明(略).
(Ⅱ)∵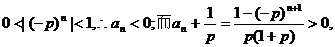
∴