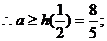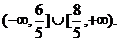【例1】如图,扇形AOB的半径为1, 中心角为45°,矩形EFGH内接于扇形, 求矩形对角线长的最小值.
[解析]这是一道高考题,需要用函数思想解决它, 但是取什么量作自变量是解决这个问题的关键,应
试题详情>>
[评析]该问题的难点是正确选择自变量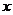 ,上面两种解法各有优缺点,解法一虽然简单些,但选择”角”作自变量有时会涉及到过多的三角知识,在许多情况下会出现困难的运算,应慎重;解法二选择矩形的边长为自变量的想法要常规一些. ,上面两种解法各有优缺点,解法一虽然简单些,但选择”角”作自变量有时会涉及到过多的三角知识,在许多情况下会出现困难的运算,应慎重;解法二选择矩形的边长为自变量的想法要常规一些. 【例2】已知正四棱锥边长为3,求它的体积的最大值.
试题详情>>
等号成立时,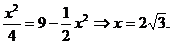 [评析]立体几何中的最值综合问题是高中数学中的一种重要题型,在立几的复习中将会作更多的讨论.
试题详情>>
(Ⅱ)若矩形ABCD的两个顶点A、B在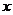 轴上,另两个顶点C、D在函数 轴上,另两个顶点C、D在函数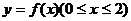 的图象上,求这个矩形面积的最大值. 的图象上,求这个矩形面积的最大值.
试题详情>>
试题详情>>
[评析]这是代数与几何的综合型的最值问题,由于这种问题能综合考核较多的数学能力,因此这是常见的试题形式,在该问题中求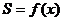 的值域时,换元这一步是很重要的想法,这样大大降低了运算量. 的值域时,换元这一步是很重要的想法,这样大大降低了运算量.
试题详情>>
试题详情>>
由条件知: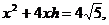 即 即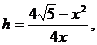 设外接圆的半径为R,即求R的最小值,
试题详情>>
此时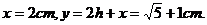 [评析]这是最值的应用问题,在函数型的应用问题中,最值应用问题占了很大的比例,也是紧常见的应用题的试题形式,应多加强这方面的训练. (一)知识归纳:
试题详情>>
1.“恒成立”问题:“设函数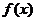 的定义域为区间D, 的定义域为区间D,
试题详情>>
1.“恒成立”与“存在”是参数讨论中的两类非常重要的问题,而通过求函数的最值是解决这两类问题的重要方法,在具体解决问题时又有两条基本思路: ①将“参数”与“变量”分离在不等号的两边,然后变量形成的函数的最值; ②“参数”与“变量”不分离,将整个式子看成一个函数,并求它的最值.
试题详情>>
2.必须注意,如果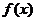 在定义区间D上没有最大或最小值,而只有上限或下限,则最后的结果可能要将“<(>)”改为“≤(≥)”. 在定义区间D上没有最大或最小值,而只有上限或下限,则最后的结果可能要将“<(>)”改为“≤(≥)”.
试题详情>>
试题详情>>
[解析]曲线的公共点为方程组的解,命题最终化归为二次方程的判断式“ 对 对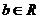 恒成立”. 恒成立”.
试题详情>>
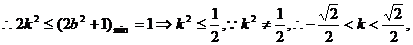 [评析]这是高考中的一道基础型试题,如果对“恒成立”的概念与方法很熟悉,则问题解答得心应手.
试题详情>>
试题详情>>
试题详情>>
[解析] A≠ 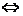 不等式 不等式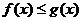 有角,这是“存在”性问题. 有角,这是“存在”性问题.
试题详情>>
试题详情>>
[解析] 这是关于“存在”性问题,注意问题中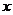 是变量, 是变量, 是参数. 是参数.
试题详情>>
显然正确,故存在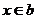 ,使得 ,使得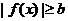 . . [评析]如果从“存在”的思想方法来理解并解答该问题,则解题思路非常清晰,才能写出上面既简洁,又严密的解题过程. 《训练题》
试题详情>>
6.设数列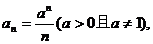 若 若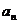 的每一项总小于它的后面的项,则 的每一项总小于它的后面的项,则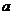 的取值范围是 的取值范围是 ( )
试题详情>>
7.若不等式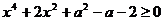 对任意实数 对任意实数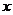 恒成立,则实数 恒成立,则实数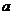 的取值范围是 的取值范围是 .
试题详情>>
10.在一块半径为R的半圆形铁皮中截出一块矩形,矩形的一边在半圆的直径上,则这个矩形的最大面积是
.
试题详情>>
12.由点P(0,1)引圆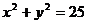 的割线与该圆交于A、B两点,求△AOB的面积的最大值(O为原点)及此时割线AB的方程. 的割线与该圆交于A、B两点,求△AOB的面积的最大值(O为原点)及此时割线AB的方程.
试题详情>>
已测定:车速为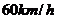 时,安全车距为 时,安全车距为 问应规定怎样的车速可使同一股道上的车流量最大?(车流量即单位时间内通过的车辆数).
试题详情>>
(Ⅱ)若函数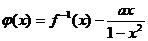 在 在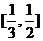 上是单调函数,求实数 上是单调函数,求实数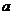 的取值范围. 的取值范围. 《答案与解析》
试题详情>>
14.命题等价于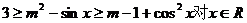 恒成立, 恒成立,
| | | | | | | | | | | | | |
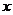 作自变量,根据问题的条件将问题转化为函数,建立函数的解析式
作自变量,根据问题的条件将问题转化为函数,建立函数的解析式 ,并求函数的(实际型)定义域;
,并求函数的(实际型)定义域; 的极值,并结合函数的定义域得到函数的最值;
的极值,并结合函数的定义域得到函数的最值;

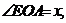
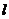 表示成这个角
表示成这个角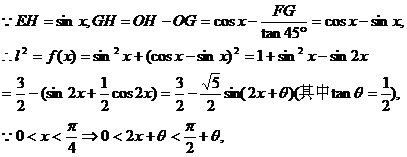
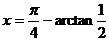 时,
时,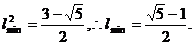
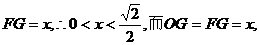
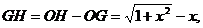
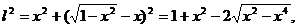
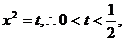
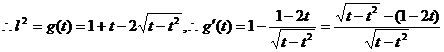
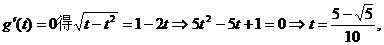
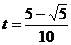 的左、右两侧取定义域内两点,如取
的左、右两侧取定义域内两点,如取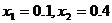
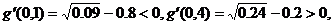
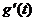 的值在
的值在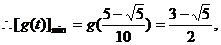
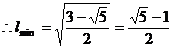 .
.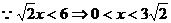
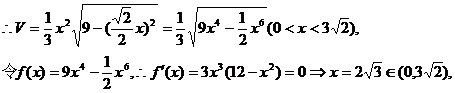
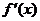 左正右负,∴当
左正右负,∴当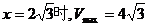 .
.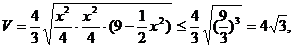
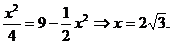
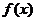 是定义在
是定义在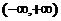 上以2为周期的周期函数,且
上以2为周期的周期函数,且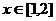 时
时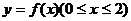 的图象上,求这个矩形面积的最大值.
的图象上,求这个矩形面积的最大值.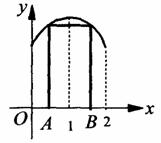
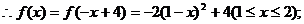
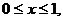 则
则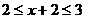 ,
, 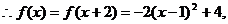
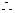 当
当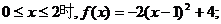

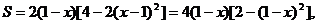
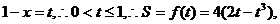
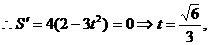 且
且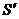 左正右负,
左正右负,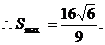
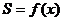 的值域时,换元这一步是很重要的想法,这样大大降低了运算量.
的值域时,换元这一步是很重要的想法,这样大大降低了运算量.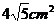 的面积,问应如何设计十字型宽
的面积,问应如何设计十字型宽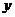 ,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.
,才能使其外接圆的周长最短,这样可使绕在铁芯上的铜线最节省.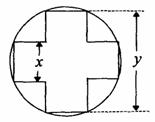
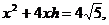 即
即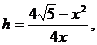
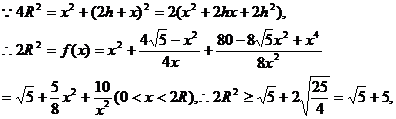
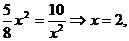
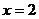 时R2最小,即R最小,从而周长
时R2最小,即R最小,从而周长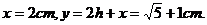
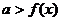 对
对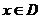 恒成立
恒成立
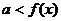 对
对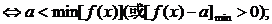
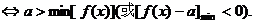

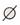
 取何值,直线
取何值,直线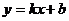 与双曲线
与双曲线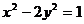 总有公共点,求实数
总有公共点,求实数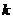 的取值范围.
的取值范围. 对
对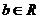 恒成立”.
恒成立”.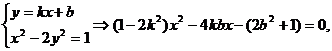
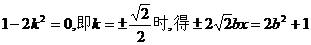 ,显然当
,显然当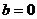 时方程无解,命题不成立;
时方程无解,命题不成立;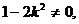 方程为一元二次方程,
方程为一元二次方程,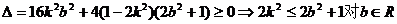 恒成立,
恒成立,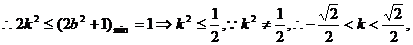
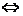 不等式
不等式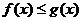 有角,这是“存在”性问题.
有角,这是“存在”性问题.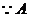 ≠
≠ 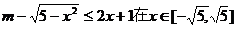 内有解,
内有解,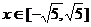 ,使得
,使得



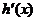 的值在
的值在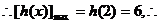 实数
实数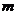 的取值范围是
的取值范围是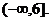
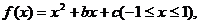 若
若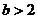 ,问是否存在
,问是否存在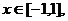 使得
使得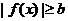 ?说明理由.
?说明理由.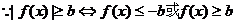 ,
,
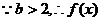 的对称轴
的对称轴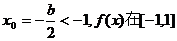 内单调递增,
内单调递增,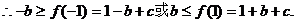 得
得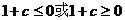 ,
,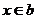 ,使得
,使得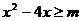 对任意
对任意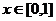 恒成立,则实数
恒成立,则实数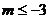 B.
B.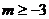
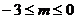 D.
D.
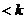 成立,则实数
成立,则实数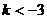 B.
B.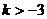 C.
C.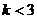 D.
D.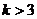
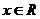 ,如果
,如果 恒成立,那么 ( )
恒成立,那么 ( )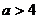 B.
B.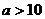 C.
C.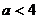 D.
D.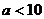
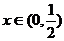 时总有
时总有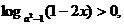 则实数
则实数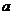 的取值范围是 ( )
的取值范围是 ( )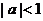 B.
B. C.
C. D.
D.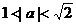
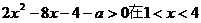 内有解,则实数
内有解,则实数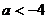 B.
B.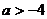 C.
C.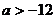 D.
D.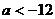
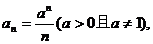 若
若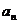 的每一项总小于它的后面的项,则
的每一项总小于它的后面的项,则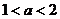 B.
B.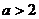 C.
C.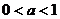 D.
D.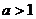
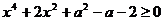 对任意实数
对任意实数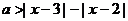 的解集为空集,则实数
的解集为空集,则实数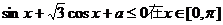 内有解,则实数
内有解,则实数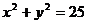 的割线与该圆交于A、B两点,求△AOB的面积的最大值(O为原点)及此时割线AB的方程.
的割线与该圆交于A、B两点,求△AOB的面积的最大值(O为原点)及此时割线AB的方程.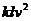 ,其中
,其中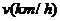 是车速,
是车速,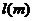 是平均车身长度,
是平均车身长度,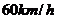 时,安全车距为
时,安全车距为
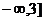 的单调减函数
的单调减函数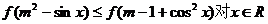 恒成立,求
恒成立,求
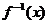 ;
;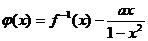 在
在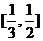 上是单调函数,求实数
上是单调函数,求实数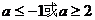 , 8.
, 8.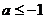 , 9.
, 9.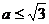 ,10.R2 .
,10.R2 .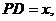 底半径为
底半径为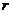 ,
,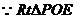 ∽
∽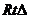 PAD,且OE=OD=1,
PAD,且OE=OD=1,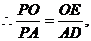 即
即
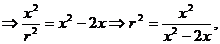

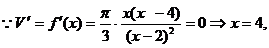
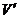 的值在
的值在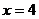 处左负右正,
处左负右正,
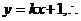 O到AB的距离
O到AB的距离
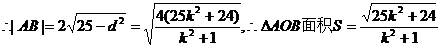

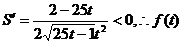 单调递减,
单调递减,
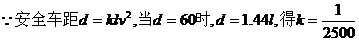 ,
,
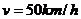 时等号成立. 当
时等号成立. 当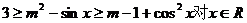 恒成立,
恒成立, ③;
③;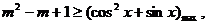

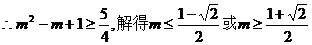 ④;
④;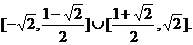
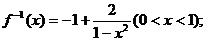
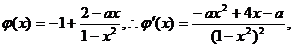
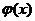 在
在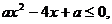 即
即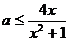 对于
对于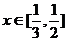 恒成立,记
恒成立,记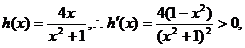
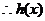 在
在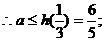
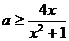 对
对