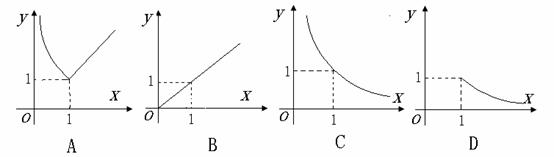
1.右图中阴影部分表示的集合是
A.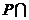
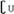
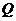 B.
B.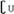
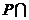
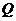
C.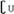 (
(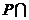
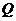 ) D.
) D.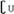 (
(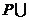
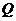 )
)
2.用反证法证明命题:若P则q ,其第一步是反设命题的结论不成立,这个正确的反设是
A.若P则非q B.若非P则q C.非P D.非q
3.已知数列{an}的通项公式为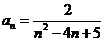 则{an}的最大项是
则{an}的最大项是
A.a1 B.a2 C.a3 D.a4
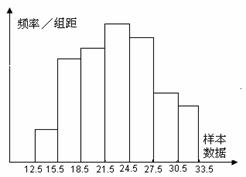 4.右图是一个样本容量为50的样本频率分布直方图,据此估计数据落在[15.5,24.5]的概率约为
4.右图是一个样本容量为50的样本频率分布直方图,据此估计数据落在[15.5,24.5]的概率约为
A.36%
B.46%
C.56%
D.66%
5.设{an}是递增等差数列,前三项的和是12,前三项的积为48,则它的首项是
A.1 B.2 C.4 D.6
6.设a> 0,a≠ 1,若y = ax的反函数的图象经过点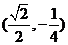 ,则a=
,则a=
A.16 B.2 C.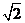 D.4
D.4
7.若函数f(x)的图象经过点 A 、(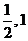 ) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是
) B、(1,0), C、(2,-1),则不能作为函数f(x)的解析式的是
A.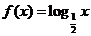 B.
B.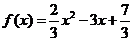
C.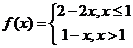 D.
D.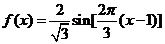
8.已知定义在R上的奇函数f (x) 满足 f (x+2) = - f (x),则f (6) 的值为
A.2 B.1 C.0 D.-1
9.函数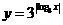 的图象大致是
的图象大致是
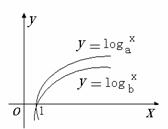 10.对数函数
10.对数函数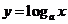 和
和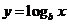 的图象如图所示,则a 、b的取值范围是
的图象如图所示,则a 、b的取值范围是
A.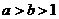
B.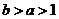
C.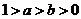
D.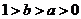
11.“a=(1,2)”是方程 “ x2y + y -2ax = 0 的曲线关于原点对称”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
12.函数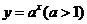 及其反函数的图象与函数
及其反函数的图象与函数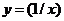 的图象交于A、B两点,若
的图象交于A、B两点,若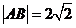 ,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈ 0.3827
lg 8.392 ≈ 0.9293 lg
8.41 ≈ 0.9247 )
,则实数a的值等于(精确到0.1 ,参考数据 lg2.414 ≈ 0.3827
lg 8.392 ≈ 0.9293 lg
8.41 ≈ 0.9247 )
A.3.8
B.
第Ⅱ卷(非选择题 共90分)
13.若 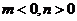 ,则
,则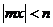 的解集是
的解集是
14.化简: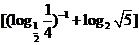 =_____________
=_____________
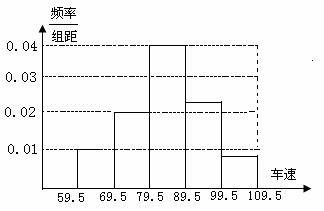 15.某路段检查站监控录象显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,分析的结果表示为如下的频率分布直方图,则估计在这一时段内通过该站的汽车中车速度不小于
15.某路段检查站监控录象显示,在某时段内,有1000辆汽车通过该站,现在随机抽取其中的200辆汽车进行车速分析,分析的结果表示为如下的频率分布直方图,则估计在这一时段内通过该站的汽车中车速度不小于
16.函数 y = ㄏ2x - 1ㄏ - ㄏx - 1ㄏ在区间 0 ≤ x ≤ 2 的最小值 。
17.(本小题满分12分)
解不等式 :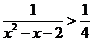
18.(本小题满分12分)
已知函数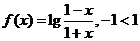 给出下列结论:
给出下列结论:
①f (x)是奇函数;②f (x)在(-1,1)内是增函数;
③ 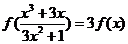 。
。
试判断这些结论的正确性,并说明理由。
19.(本小题满分12分)
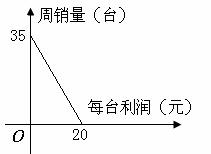 商品营销中,商品的质量与它的利润直接相关。某电器商店发现某种型号的函数计数器的周销售量与每台的利润间的一次函数关系如图所示。问:周销售量为多少时,可使商店获得的利润最大?(结果精确到 0.1)。
商品营销中,商品的质量与它的利润直接相关。某电器商店发现某种型号的函数计数器的周销售量与每台的利润间的一次函数关系如图所示。问:周销售量为多少时,可使商店获得的利润最大?(结果精确到 0.1)。
20.(本小题满分12分)
某农场在相同条件下种植甲、乙两种水稻各100 亩,它们的收获情况如下:
甲 乙
亩产量(单位:千克)
300
320
330
340
亩数
20
25
40
15
亩产量(单位:千克)
310
320
330
340
亩数
30
20
40
10
试说明哪种水稻的产量比较稳定?
21.(本小题满分12分)
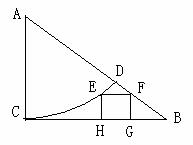 在△ABC中,∠C = 90o ,BC = 1.以A为圆心,AC为半径画弧交AB于D,在由弧CD与直线段BD、BC所围成的范围内作内接正方形EFGH(如图)。设AC = x,EF = y ,
在△ABC中,∠C = 90o ,BC = 1.以A为圆心,AC为半径画弧交AB于D,在由弧CD与直线段BD、BC所围成的范围内作内接正方形EFGH(如图)。设AC = x,EF = y ,
(1)求y与x的函数关系式;
(2)正方形EFGH的面积是否有最大值?试证明你的结论。
22.(本小题满分14分)
a 为常数,求函数 的最大值。
的最大值。