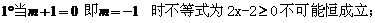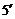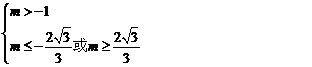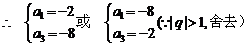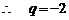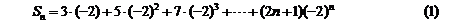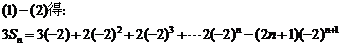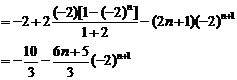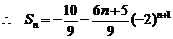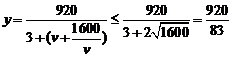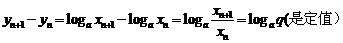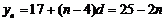1.设等差数列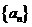 的前
的前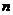 项和为
项和为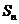 ,若
,若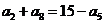 ,则
,则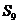 等于……………
等于……………
A.18
B.
2.在△ABC中,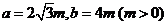 ,如果三角形有解,则A的取值范围是…
,如果三角形有解,则A的取值范围是…
A.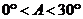 B.
B.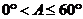 C.
C.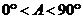 D.
D.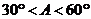
3.已知数列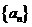 满足
满足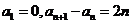 ,那么
,那么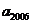 的值为………………………
的值为………………………
A.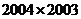 B.
B.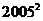 C.
C. 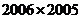 D.
D. 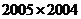
4.不等式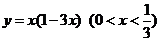 的最大值是……………………………………
的最大值是……………………………………
A.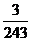 B.
B. 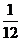 C.
C. 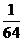 D.
D. 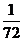
5.已知等比数列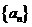 中,
中,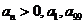 为方程
为方程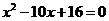 的两根,则
的两根,则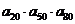 的值为……………………………………………………………………………………
的值为……………………………………………………………………………………
A.32
B. 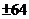
6.下列命题中正确的是…………………………………………………………………
A.
函数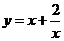 的最小值为
的最小值为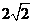
B.函数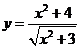 的最小值为2 .
的最小值为2 .
C.函数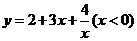 的最大值为
的最大值为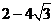 .
.
D.函数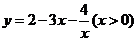 的最小值为
的最小值为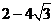 .
.
7.在△ABC中,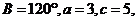 则
则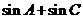 的值为………………………
的值为………………………
A.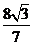 B.
B.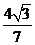 C.
C. 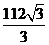 D.
D. 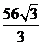
8.已知等比数列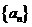 的各项均为正数,公比
的各项均为正数,公比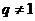 ,设
,设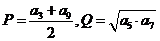 ,则
,则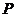 与
与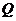 的大小关系是…………………………………………………………………………
的大小关系是…………………………………………………………………………
A.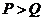 B.
B.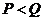 C.
C.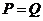 D.无法确定
D.无法确定
9.设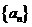 是等比数列,有下列四个命题:①数列
是等比数列,有下列四个命题:①数列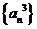 是等比数列 ②数列
是等比数列 ②数列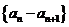 是等比数列③数列
是等比数列③数列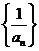 是等比数列 ④ 数列
是等比数列 ④ 数列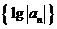 是等比数列. 其中正确的命题个数为…………………………………………………………………………………………
是等比数列. 其中正确的命题个数为…………………………………………………………………………………………
A.1
B.
10.若不等式 对任意实数
对任意实数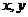 都成立,则实数
都成立,则实数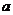 的取值范围是…………………………………………………………………………………………
的取值范围是…………………………………………………………………………………………
A.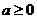 B.
B.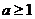 C.
C.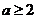 D.
D.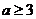
第Ⅱ卷(非选择题 共100分)
11.已知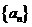 是等差数列,且公差
是等差数列,且公差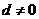 ,又
,又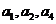 依次成等比数列,则
依次成等比数列,则
 =______▲_________.
=______▲_________.
12. .
.
13.已知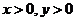 且
且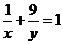 ,则
,则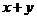 的最小值为_______▲___________.
的最小值为_______▲___________.
14.已知△ABC的面积为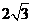 ,AB=2,BC = 4,则三角形的外接圆半径为____▲_________.
,AB=2,BC = 4,则三角形的外接圆半径为____▲_________.
15.已知a>0,b>0且a+b+2=ab,则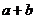 的取值范围是___▲____.
的取值范围是___▲____.
16.等差数列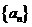 的公差d不为0,
的公差d不为0,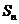 是其前
是其前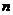 项和,有以下四个命题
项和,有以下四个命题
①若d<0,且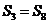 ,则数列
,则数列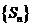 中
中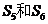 都是
都是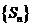 中的最大项;
中的最大项;
②给定n≥2,对于一切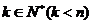 都有
都有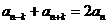 ;
;
③若d>0,则数列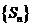 中一定有数值最小的项;
中一定有数值最小的项;
④ 存在 ,使
,使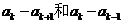 同号.
同号.
其中 的序号有_____▲_______.(填上你认为错误的所有命题的序号.)
的序号有_____▲_______.(填上你认为错误的所有命题的序号.)
17.(本小题14分)函数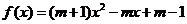 的定义域为R,函数值均为非负数,求实数
的定义域为R,函数值均为非负数,求实数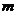 的取值范围.
的取值范围.
18.(本小题14分) 已知在△ABC中,
(1)若三边长a,b,c依次成等差数列,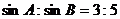 ,求三个内角中最大角的度数;
,求三个内角中最大角的度数;
(2)若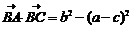 ,求cosB.
,求cosB.
19.(本小题14分)
已知数列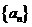 是等比数列,且
是等比数列,且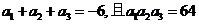 ,
,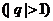
(1) 求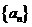 的通项公式;
的通项公式;
(2) 令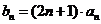 ,求数列
,求数列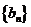 的前n项和的公式.
的前n项和的公式.
20. (本小题14分)
经过长期观测得到:在交通繁忙的时段内,某公路汽车的车流量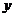 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度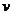 (千米/小时)之间的函数关系为
(千米/小时)之间的函数关系为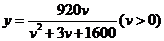
(1) 在该时段内,当汽车的平均速度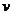 为多少时,车流量最大?最大为多少?(精确到0.1千辆/小时)
为多少时,车流量最大?最大为多少?(精确到0.1千辆/小时)
(2) 若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
21. (本小题14分)
等比数列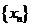 各项均为正值,
各项均为正值,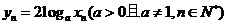 ,已知
,已知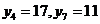
(1) 求证:数列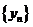 是等差数列;
是等差数列;
(2) 数列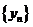 的前多少项的和为最大?最大值是多少?
的前多少项的和为最大?最大值是多少?
(3) 求数列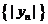 的前
的前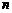 项和.
项和.
通州市2005――2006学年(下)高一期中联考
数 学 试 卷 答 案
CBCBB CBABC
11.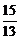 12.
12.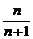 13.16
14. 2 或
13.16
14. 2 或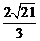
15. 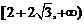 16.
④
16.
④
17.问题转化为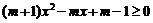 对任意实数
对任意实数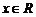 恒成立.
恒成立. 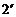
综上所述: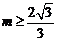
18. 在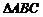 中有sinA:sinB=3:5
中有sinA:sinB=3:5
∴a : b=3 : 5 2′
令a = 3k (k>0) ∴ b = 5k
∵a,b,c成等差数列 ∴ c =7k
∴最大角为C,有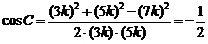 5′
5′
C=120° 7′
(2)由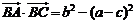
得 accosB=b2-(a-c)2 9′
即accosB=a2+c2-2accosB-(a2+c2-2ac) 11′
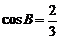 14′
14′
19.(1)由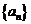 是等比数列且
是等比数列且
得 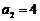
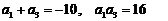
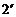
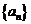 的通项公式
的通项公式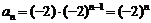 7′
7′
(2) 设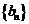 的前n项和为
的前n项和为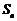
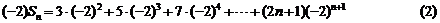 9′
9′
20.(1)依题意
当且仅当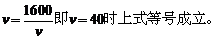
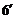
所以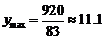 (千辆/小时)
(千辆/小时)
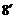
(2) 由条件得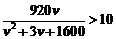
整理得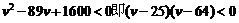
解得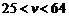 .
.
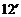
答:当千米/小时是,车流量最大,最大车流量约为11.1千辆/小时.如果要求在该段时段内车流量超过10千辆/小时,则汽车的平均速度应大于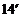 21.(1)
21.(1)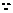
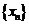 是等比数列,设其公比为
是等比数列,设其公比为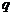 ,则
,则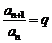 (定值)
(定值)
所以数列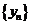 是等差数列.
是等差数列.
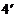
(2)由(1)知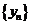 是等差数列,
是等差数列,
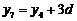 即
即 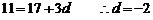
由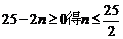
当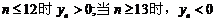
所以数列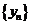 的前12项和最大;
的前12项和最大;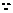
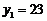
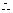 最大值
最大值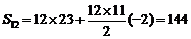 9′
9′
(3)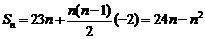

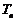 ,
,
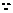 当
当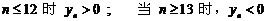
当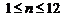 时
时 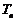 =
=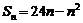 11′
11′
当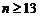 时,
时,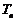 =
=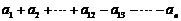
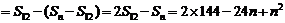 13′
13′
所以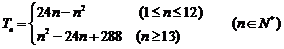
 2005――2006学年(下)期中联考
2005――2006学年(下)期中联考
高 一 数 学 (B卷)
题 号
二
三
总分
17
18
19
20
21
得 分
评卷人
11. ;
12. ;
13. ;
14. ;
15. ;
16. .
17.(14分)
18. (14分)
19. (14分)
20. (14分)
21. (14分)