1.甲:A1、A2是互斥事件;乙:A1、A2是对立事件,那么
A.甲是乙的充分但不必要条件 B.甲是乙的必要但不充分条件
C.甲是乙的充要条件 D.甲既不是乙的充分条件,也不是乙的必要条件
2.若 、
、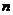 表示直线,
表示直线, 表示平面,则下列命题中,正确的个数为
表示平面,则下列命题中,正确的个数为
①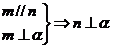 ②
② ③
③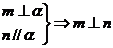 ④
④
A.1个 B.2个 C.3个 D.4个
3.从8名女生,4名男生中选出6名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法种数为
A.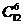 B.
B.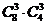 C.
C.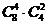 D.
D.
4.过半径为2的球O表面上一点A作球O的截面,若OA与该截面所成的角是60°则该截面的面积是
A.π
B.2π C.3π
D.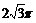
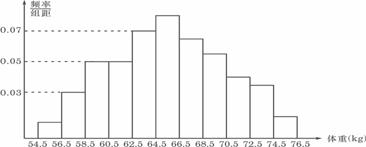
5.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是
A.20
B.
6.甲、乙、丙3位同学用计算机联网学习数学,每天上课后独立完成6道自我检测题,甲答及格的概率为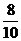 ,乙答及格的概率为
,乙答及格的概率为 ,丙答及格的概率为
,丙答及格的概率为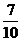 ,3人各答1次,则3人中只有1人答及格的概率为
,3人各答1次,则3人中只有1人答及格的概率为
A. B.
B.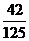 C.
C.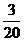 D.
D.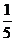
 7.4名男生3名女生排成一排,若3名女生中有2名站在一起,但3名女生不能全排在一起,则不同的排法种数有
7.4名男生3名女生排成一排,若3名女生中有2名站在一起,但3名女生不能全排在一起,则不同的排法种数有
A.1440
B.
8.如图,正三棱柱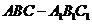 的各棱长都2,E,F分别是
的各棱长都2,E,F分别是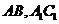 的中点,则EF的长是
的中点,则EF的长是
A.2
B. C.
C. 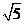 D.
D.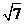
9. 已知 ,且关于
,且关于 的方程
的方程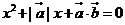 有实根,则
有实根,则 与
与 的夹角的取值范围是
的夹角的取值范围是
A.[0, ] B.
] B. C.
C. D.
D.
10.对于任意的两个实数对 和
和 ,规定:
,规定: ,当且仅当
,当且仅当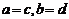 ;运算“
;运算“ ”为:
”为: ;运算“
;运算“ ”为:
”为: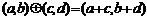 ,设
,设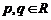 ,若
,若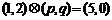 ,则
,则
A. B.
B.  C.
C.  D.
D. 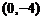
第Ⅱ卷(非选择题 共100分)
11.已知向量 ,
, ,则
,则 的最大值为
_____▲____。
的最大值为
_____▲____。
12.接种某疫苗后,出现发热反应的概率为0.80,现有5人接种了该疫苗,至少有3人出现发热反应的概率为 __▲__ 。(精确到0.01)
13.设离散型随机变量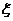 可能取的值为1,2,3,4。
可能取的值为1,2,3,4。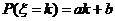 (
( 1,2,3,4)。又
1,2,3,4)。又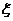 的数学期望
的数学期望 ,则
,则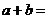 ▲ 。
▲ 。
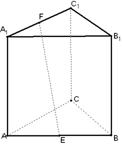
14.如图,正方体ABCD-A1B
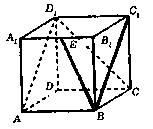 ①点E到平面ABC1D1的距离是
①点E到平面ABC1D1的距离是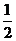 ;
;
②直线BC与平面ABC1D1所成角等于45°;
③空间四边形ABCD1,在正方体六个面内的射影围成面积最小值为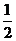 ;
;
④BE与CD1所成角为arcsin .
.
其中真命题的编号是___▲_____(写出有真命题的编号)
15.(本小题满分14分)
在二项式 中,如果它的展开式里系数最大的项恰好是不含x的常数项;
中,如果它的展开式里系数最大的项恰好是不含x的常数项;
(1)问常数项是第几项?
(2)求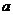 的取值范围.
的取值范围.
16.(本小题满分14分)
已知7件产品中有4件正品和3件次品.
(1)从这7件产品中一次性随机抽取3件,求正品件数不少于次品件数的概率;
(2)从这7件产品中一次性随机抽取5件,记其中次品件数为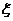 ,求
,求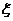 的数学期望。
的数学期望。
17.(本小题满分14分)
甲、乙、丙3人投篮,投进的概率分别是, , .
(1)现3人各投篮1次,求3人都没有投进的概率;
(2)用ξ表示乙投篮3次的进球数,求随机变量ξ的概率分布及数学期望Eξ.
18.(本小题满分14分)
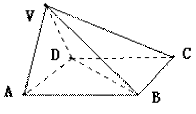 在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD.
(1)证明AB⊥平面VAD;
(2)求面VAD与面VDB所成的二面角的大小.
19.(本题满分14分)
设 .
.
(1)求 ,
,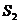 ,
, ,
,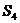 的值,并据此猜测数列
的值,并据此猜测数列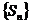 的通项公式;
的通项公式;
(2)用数学归纳法证明你的猜测.
20.(本小题满分14分)
从原点出发的某质点M,按向量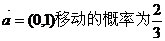 ,按向量
,按向量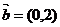 移动的概率为
移动的概率为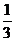 ,设M可到达点(0,n)的概率为Pn.
,设M可到达点(0,n)的概率为Pn.
(1)求P1和P2的值;
(2)求证: ;
;
(3)求Pn的表达式.