【题目】如图所示，在水平线ab的下方有一匀强电场，电场强度为E，方向竖直向下，ab的上方存在匀强磁场，磁感应强度为B，方向垂直纸面向里，磁场中有一内、外半径分别为R、的半圆环形区域，外圆与ab的交点分别为M、N。一质量为m、电荷量为q的带负电粒子在电场中P点静止释放，由M进入磁场，从N射出，不计粒子重力。学科.网

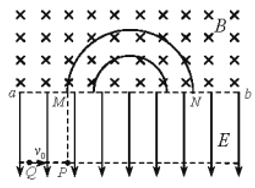
（1）求粒子从P到M所用的时间t；

（2）若粒子从与P同一水平线上的Q点水平射出，同样能由M进入磁场，从N射出，粒子从M到N的过程中，始终在环形区域中运动，且所用的时间最少，求粒子在Q时速度的大小。

【答案】（1）（2）

【解析】试题分析：粒子在磁场中以洛伦兹力为向心力做圆周运动，在电场中做初速度为零的匀加速直线运动，据此分析运动时间；粒子进入匀强磁场后做匀速圆周运动，当轨迹与内圆相切时，所有的时间最短，粒子从Q射出后在电场中做类平抛运动，在电场方向上的分运动和从P释放后的运动情况相同，所以粒子进入磁场时沿竖直方向的速度同样为v，结合几何知识求解．

（1）设粒子在磁场中运动的速度大小为v，所受洛伦兹力提供向心力，有①

设粒子在电场中运动所受电场力为F，有F=qE②；

设粒子在电场中运动的加速度为a，根据牛顿第二定律有F=ma③；

粒子在电场中做初速度为零的匀加速直线运动，有v=at④；联立①②③④式得⑤；

（2）粒子进入匀强磁场后做匀速圆周运动，其周期与速度、半径无关，运动时间只由粒子所通过的圆弧所对的圆心角的大小决定，故当轨迹与内圆相切时，所有的时间最短，设粒子在磁场中的轨迹半径为，由几何关系可得⑥

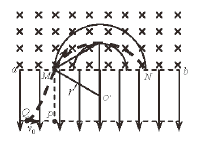
设粒子进入磁场时速度方向与ab的夹角为θ，即圆弧所对圆心角的一半，由几何关系知⑦；

粒子从Q射出后在电场中做类平抛运动，在电场方向上的分运动和从P释放后的运动情况相同，所以粒子进入磁场时沿竖直方向的速度同样为v，在垂直于电场方向的分速度等于为，由运动的合成和分解可得⑧

联立①⑥⑦⑧式得⑨．

关闭