【题目】如图甲所示,一质量为M的长木板静置于光滑水平面上,其上放置一质量为m小滑块.木板受到随时间t变化的水平拉力F作用时,用传感器测出长木板的加速度a与水平拉力F的关系如图乙所示,取g=10m/s2,则( )

A.当0<F<6N时,滑块与木板之间的摩擦力随F变化的函数关系f=2F/3
B.当F=8N时,滑块的加速度为1m/s2
C.滑块与木板之间的滑动摩擦因素为0.2
D.力随时间变化的函数关系一定可以表示为F=6t(N)
参考答案:
【答案】AB
【解析】
试题分析:当F等于6N时,加速度为:a=1m/s2,对整体分析,由牛顿第二定律有:F=(M+m)a,代入数据解得:M+m=6kg,当F大于6N时,根据牛顿第二定律得:![]() ,图象斜率
,图象斜率![]() ,解得:M=2kg,滑块的质量m=4kg,由牛顿第二定律得,对系统:F=(M+m)a,对m:f=ma,解得:f=
,解得:M=2kg,滑块的质量m=4kg,由牛顿第二定律得,对系统:F=(M+m)a,对m:f=ma,解得:f=![]() F,故A正确;根据F大于6N的图线知,F=4时,a=0,即:
F,故A正确;根据F大于6N的图线知,F=4时,a=0,即:![]() ,解得:μ=0.1,a=
,解得:μ=0.1,a=![]() F-2,当F=8N时,长木板的加速度为:a=2m/s2;根据μmg=ma′得:滑块的加速度为 a′=μg=1m/s2,故B正确,C错误.当M与m共同加速运动时,加速度相同,加速度与时间的关系为:力随时间变化的函数关系一定可以表示为F=6t(N),当F大于6N后,发生相对滑动,表达式不是F=6t,故D错误;故选AB。
F-2,当F=8N时,长木板的加速度为:a=2m/s2;根据μmg=ma′得:滑块的加速度为 a′=μg=1m/s2,故B正确,C错误.当M与m共同加速运动时,加速度相同,加速度与时间的关系为:力随时间变化的函数关系一定可以表示为F=6t(N),当F大于6N后,发生相对滑动,表达式不是F=6t,故D错误;故选AB。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在光滑的斜面上自由下滑的物体受到的力是( )
A.重力和斜面的支持力
B.重力、下滑力
C.重力,下滑力和斜面的支持力
D.重力垂直斜面的分力就是它对斜面的压力 -
科目: 来源: 题型:
查看答案和解析>>【题目】力的合成与分解实际是等效代换,合力和它的分力的作用效果应当是相同的,在“验证力的平行四边形定则”中,合力和分力的作用效果是( )
A.把弹簧秤拉到同一刻度
B.把橡皮条拉到不同长度
C.把橡皮条系细绳的一端拉到同一点
D.把弹簧秤拉到最大刻度 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图一根不可伸长绝缘的细线一端固定于O点,另一端系一带电小球,置于水平向右的匀强电场中,现把细线水平拉直,小球从A点静止释放,经最低点B后,小球摆到C点时速度为0,则( )
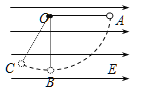
A.小球在B点时的速度最大
B.小球从A到B的过程中,机械能一直在减少
C.小球在B点时的绳子拉力最大
D.从B到C的过程中小球的电势能一直增大
-
科目: 来源: 题型:
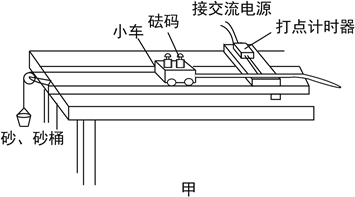
查看答案和解析>>【题目】图甲为“探究加速度与物体所受力合外力、物体质量的关系”的实验装置示意图,砂和砂桶的总质量为
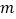 ,小车和砝码的总质量为
,小车和砝码的总质量为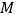 .
.

(
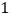 )如图乙所示为实验中用打点计时器打出的一条较理想的纸事,打点计时器所用交流电的频率为
)如图乙所示为实验中用打点计时器打出的一条较理想的纸事,打点计时器所用交流电的频率为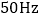 ,纸带上
,纸带上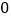 、
、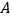 、
、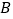 、
、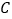 、
、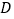 、
、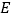 为六个相邻的计数点(两相邻计数点间还有
为六个相邻的计数点(两相邻计数点间还有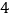 个点迹没有画出),通过测量和计算可知,
个点迹没有画出),通过测量和计算可知,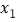 、
、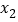 、
、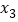 、
、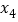 、
、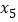 分别为
分别为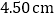 、
、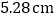 、
、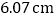 、
、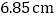 、
、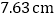 ,则打点计时器打下相邻计数点的时间间隔为__________
,则打点计时器打下相邻计数点的时间间隔为__________ ,根据上述数据,可知小车拖动纸带运动的加速度的测量值为__________
,根据上述数据,可知小车拖动纸带运动的加速度的测量值为__________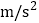 (保留
(保留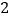 位有效数字).
位有效数字).(
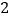 )实验中用砂和砂桶总重力的大小作为细线对小车拉力的大小,在探究外力不变的情况下加速度与质量之间的关系时,用到了小车的加速度
)实验中用砂和砂桶总重力的大小作为细线对小车拉力的大小,在探究外力不变的情况下加速度与质量之间的关系时,用到了小车的加速度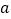 与小车和砝码总质量的倒数关系的图像.以下关于该实验的说法中正确的是__________.(选填选项前的字母)
与小车和砝码总质量的倒数关系的图像.以下关于该实验的说法中正确的是__________.(选填选项前的字母)A.需要用天平测量小车和砝码的总质量
B.实验需要保证的条件是小车和砝码的总质量远大于砂和砂桶的总质量
C.实验前需要将固定打点计时器一侧的木板垫高一些,其目的是增大小车下滑的加速度
D.实验时如果没有将固定打点计时器一侧的木板垫高一些,会导致小车的加速度
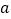 与小车和砝码总质量的倒数关系图像(
与小车和砝码总质量的倒数关系图像( 图像)不是一条直线.
图像)不是一条直线. -
科目: 来源: 题型:
查看答案和解析>>【题目】伽利略对自由落体运动研究中,经历了提出问题、科学猜想、数学推理、实验验证、合理外推、得出结论一系列过程.其中在实验验证过程中,他让一个铜球沿阻力很小的斜面滚下,来“冲淡”重力,为什么要“冲淡”重力,“冲淡”重力的含义是什么( )
A.减小重力
B.减小运动速度
C.增加运动时间
D.便于测量运动位移 -
科目: 来源: 题型:
查看答案和解析>>【题目】(9分)某研究性学习小组的同学们做了以下两个关于弹簧的实验。
(1)在做探究弹簧弹力的大小与其伸长量的关系实验中,设计了如图所示的实验装置。在弹簧两端各系一轻细的绳套,利用一个绳套将弹簧悬挂在铁架台上,另一端的绳套用来悬挂钩码。同学们先测出不挂钩码时弹簧的长度,再将钩码逐个挂在弹簧的下端,每次都测出相应的弹簧总长度L,再算出弹簧伸长的长度x,并将数据填在下面的表格中。(实验过程中,弹簧始终在弹性限度内)
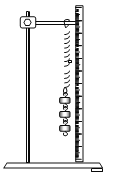
测量次序
1
2
3
4
5
6
悬挂钩码所受重力G/N
0
0.5
1.0
1.5
2.0
2.5
弹簧弹力大小F/N
0
0.5
1.0
1.5
2.0
2.5
弹簧的总长度L/cm
13.00
15.05
17.10
19.00
21.00
23.00
弹簧伸长的长度x/cm
0
2.05
4.10
6.00
8.00
10.00
①在如图所示的坐标纸上已经描出了其中5次测量的弹簧弹力大小F与弹簧伸长的长度x对应的数据点,请把第4次测量的数据对应点描绘出来,并作出F-x图线。
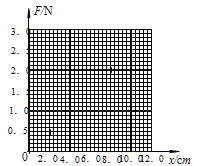
②根据上述的实验过程,并对实验数据进行分析可知,下列说法中正确的是 。(选填选项前的字母)
A.弹簧弹力大小与弹簧的总长度成正比
B.弹簧弹力大小与弹簧伸长的长度成正比
C.该弹簧的劲度系数约为25N/m
D.在不挂钩码的情况下测量弹簧的长度时,需将弹簧放置在水平桌面上测量
(2)研究性学习小组的同学将该弹簧放置在一个高度为h的水平桌面上,将其左端固定,右端与质量为m的小钢球接触。当弹簧处于自然长度时,小钢球恰好在桌子边缘,如图甲所示。将钢球向左压缩弹簧一段距离x后由静止释放,钢球将沿水平方向飞出桌面,钢球在空中飞行一段距离后落到水平地面上,测得其水平飞行距离为s。该小组的同学想用这个装置探究弹簧将钢球弹出的过程中,弹簧弹力对钢球所做的功与此过程中钢球动能增量之间的关系。
①同学们发现,当压缩弹簧的距离x不同时,钢球落地时的水平距离s也会不同。可以根据第(1)问中画出的F-x图象求出弹簧弹力对钢球所做的功,然后研究弹簧弹力对钢球所做的功W与此过程中钢球动能增量Ek之间的关系。根据这样的思路同学们预测了几种不同的s-x关系图象,图乙中可以表明弹簧弹力对钢球所做的功W等于此过程中钢球动能的增量Ek的图象是 。(选填选项下面的字母)
②在实验中发现,弹簧弹力对钢球所做的功W大于钢球的动能增量Ek。请你简述导致W大于Ek的可能原因(至少说出两条): 。
相关试题

