搜索
【题目】如图所示，两平行板间有垂直纸面向里的匀强磁场，磁感应强度为B，板长为
L，两板间距离为L。有一个带电量为q、质量为m的粒子，以水平速度v，从靠近上板边缘处进入该磁场，粒子恰能从下极板右侧边缘离开磁场，不计粒子重力。则（ ）
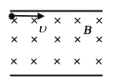
A.该粒子带正电
B.该粒子做匀变速曲线运动
C.该粒子在磁场中运动的时间为
D.该粒子离开磁场时速度偏转角为
【答案】D
【解析】
A．根据题意可知，粒子向下偏转，受到洛伦兹力向下，所以粒子带负电，故A错误；
B．根据题意粒子在磁场中做匀速圆周运动，即做变加速曲线运动，故B错误；
C．粒子在磁场中做匀速圆周运动的轨迹如图所示
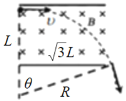
设圆周半径为R，圆心角为
，由勾股定理有
解得
故有
可知圆心角为
则速度偏向角为
，则粒子在磁场中运动的时间为
故C错误，D正确。
故选D。
