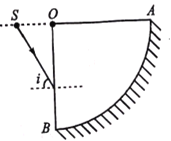
【题目】如图，ABO是一半径为R的圆形玻璃砖的横截面，O是圆心，AB弧形面镀银。现位于AO轴线上的点光源S发出一束光线射向玻璃砖的OB边，入射角i=60°，OS=。已知玻璃的折射率为，光在空气中传播的速度为c，每条边只考虑一次反射。求：

（i）光线射入玻璃砖时的折射角；

（ii）光线从S传播到离开玻璃砖所用的时间。

【答案】(i) 30°；(ii) 。

【解析】

(i)光路如答图2，设光在C点的折射角为r

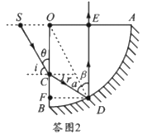
由折射定律有

代入数据解得

r=30°

(ii)进入玻璃砖中，光在AB面上D点反射，设入射角为，反射角为

=90°-i=30°

由三角函数关系有

OC=OScot=

且

在ΔODC中，由正弦定理有：

得

=30°

由于=30°，∠CDF=30°，故∠FDE=90°，所以光线DE垂直于OA射出玻璃砖

在∠ODC中，由几何关系有

CD=OC=

又

DE=Rcos=

光在玻璃中的速率

则光线从S传播到离开玻璃砖所用的时间

解得

关闭