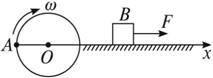
在同一水平面上有A、B两物体,它们的质量分别为m、M,A物体从如图5-4-7 所示的位置开始以角速度ω绕O点在竖直平面内沿顺时针方向做匀速圆周运动,其轨道半径为R.同时B物体在恒力F作用下,由静止开始在光滑水平面上沿x轴正方向做直线运动,如图5-4-7所示.试问:
图
(1)A物体运动到什么位置时,它的速度可能与B物体的速度相同?
(2)要使两物体速度相同,作用在B物体上的力F应为多大?
(3)当物体速度相同时,B物体的最小位移是多少?
解析:本题考查对匀速圆周运动及牛顿第二定律、运动学公式的综合理解、运用能力.在物理问题中求解周期性的物体运动,常存在多解.本题中,由于匀速圆周运动的物体具有周期性的运动特性,经分析可知A物体第一次、第二次……到达最高点都有可能与B物体具有相同的速度,因而本题将有无数组解都可满足题设要求.
(1)要使A、B两物体的速度相同,A物体必须运动到圆周最高点,此时两者的速度方向都向右.
(2)当物体A第一次到达圆周最高点时:![]()
当物体A第二次到达圆周最高点时:![]()
则当物体A第n+1次到达圆周最高点时:![]() ①
①
要使两物体速度相同,则有vA=vB,
即![]() ②
②
联立①②式可解得:![]() .
.
(3)两物体速度相同时,当n=0,此时,![]() ,
,![]() ,
,
B物体的位移sB最小,故![]()
即为所求的最小位移.

