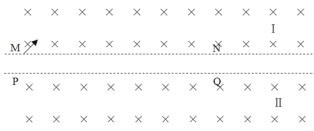
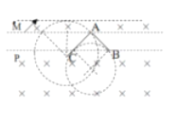
【题目】如图所示，MN 和PQ 是匀强磁场的理想边界，MN上方为匀强磁场Ⅰ，PQ下方为匀强磁场Ⅱ，MN和 PQ间距为d d ，之间区域没有场。质量为m，带电量为q的负电粒子自M点以速度v0，方向与边界夹角45°斜向右上第一次射入Ⅰ磁场，带电粒子每次穿越边界MN和PQ过程中动能可能有损失，穿越后的动能为穿越前的k倍（k≤1），已知，两部分磁场方向均垂直纸面向里，磁感强度大小均为B ，粒子的重力和空气阻力可以忽略。

(1)为了使粒子能返回 MN 边界，磁场Ⅰ的最小宽度为多大？

(2)若粒子自A点第一次离开磁场Ⅰ，为使粒子第二次进入磁场Ⅰ的位置为A点，k的值为多少？

(3)若 k=，请计算第3次到达磁场Ⅰ位置距M点的距离？

【答案】(1)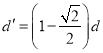；(2)；(3)

【解析】

(1)洛伦兹力提供做圆周运动的向心力，根据牛顿第二定律

所以

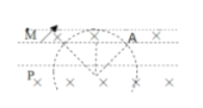
根据几何关系，Ⅰ磁场宽度d′

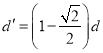
(2)粒子自A点离开磁场，与边界夹角为45°，自B点进入Ⅱ磁场，自C点离开，为了粒子能返回A点

所以

洛伦兹力提供向心力

自Ⅰ磁场进入Ⅱ磁场，两次穿越边界

解得

(3)根据题意已知，第一次进入磁场Ⅰ时粒子运动轨迹半径为d，

第一次进入磁场Ⅱ时

轨道半径

第二次进入磁场Ⅰ时

轨道半径

第二次进入磁场Ⅱ时

轨道半径

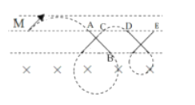
根据几何关系

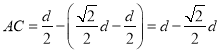
所以

关闭