搜索
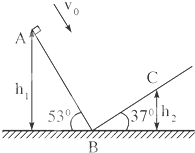
“嫦娥一号”探月卫星的成功发射，实现了中华民族千年奔月的梦想．假若我国的航天员登上某一星球并在该星球表面上做了如下图所示力学实验：让质量为m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下，到达B点后恰好能沿倾角为37°的斜面到达C点．不计滑过B点时的机械能损失，滑块与斜面间的动摩擦因数均为μ=0.5，测得A、C两点离B点所在水平面的高度分别为h1=1.2m，h2=0.5m．已知sin37°=0.6，cos37°=0.8，不计该星球的自转以及其他星球对它的作用．（1）求该星球表面的重力加速度g；
（2）若测得该星球的半径为R=6×106m，宇航员要在该星球上发射一颗探测器绕其做匀速圆周运动，则探测器运行的最大速度为多大？
（3）取地球半径R0=6.4×106m，地球表面的重力加速度g0=10m/s2，求该星球的平均密度与地球的平均密度之比
| ρ | ρ0 |
分析：（1）小滑块从A到C的过程中，对滑块进行受力分析和做功分析，根据动能定理列方程求得重力加速度；
（2）根据万有引力提供向心力、重力等于万有引力列式，求解探测器的最大速度．
（3）根据密度公式和黄金代换式GM=gR2，求解星球的平均密度与地球的平均密度之比．
（2）根据万有引力提供向心力、重力等于万有引力列式，求解探测器的最大速度．
（3）根据密度公式和黄金代换式GM=gR2，求解星球的平均密度与地球的平均密度之比．
解答：解：（1）小滑块从A到C的过程中，由动能定理得：
mg（h1-h2）-μmgcos53°•
-μmgcos37°•
=0-
m
代人数据解得：g=6m/s2
（2）设探测器质量为m′，探测器绕该星球表面做匀速圆周运动时运行最大速度，由牛顿第二定律和万有引力得：
G
=m′
又G
=mg
解得：v=
代人数据解得：v=6km/s
（3）由星球密度ρ=
和GM=gR2得该星球的平均密度与地球的平均密度之比
=
．
代人数据解得：
=0.64．
答：
（1）该星球表面的重力加速度g为6m/s2；
（2）则探测器运行的最大速度为6km/s．
（3）该星球的平均密度与地球的平均密度之比
为0.64．
mg（h1-h2）-μmgcos53°•
| h1 |
| sin53° |
| h2 |
| sin37° |
| 1 |
| 2 |
| v | 2 0 |
代人数据解得：g=6m/s2
（2）设探测器质量为m′，探测器绕该星球表面做匀速圆周运动时运行最大速度，由牛顿第二定律和万有引力得：
G
| Mm′ |
| R2 |
| v2 |
| R |
又G
| Mm |
| R2 |
解得：v=
| gR |
代人数据解得：v=6km/s
（3）由星球密度ρ=
| M | ||
|
| ρ |
| ρ0 |
| gR0 |
| g0R |
代人数据解得：
| ρ |
| ρ0 |
答：
（1）该星球表面的重力加速度g为6m/s2；
（2）则探测器运行的最大速度为6km/s．
（3）该星球的平均密度与地球的平均密度之比
| ρ |
| ρ0 |
点评：万有引力应用主要从万有引力提供圆周运动的向心力和星球表面重力和万有引力相等两方面入手分析．
