Question

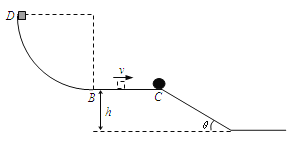
【题目】如图，半径R = 1.0m的四分之一圆弧形光滑轨道竖直放置，圆弧最低点B与长为L＝0.5m的水平面BC相切于B点，BC离地面高h = 0.45m，C点与一倾角为θ = 37°的光滑斜面连接，质量m＝1.0 kg的小滑块从圆弧上某点由静止释放，到达圆弧B点时小滑块对圆弧的压力刚好等于其重力的2倍,当小滑块运动到C点时与一个质量M=2.0kg的小球正碰，碰后返回恰好停在B点，已知滑块与水平面间的动摩擦因数＝0.1。（sin37°=0.6 cos37°=0.8, g取l0 m/s2）

求：

（1）小滑块应从圆弧上离地面多高处释放；

（2）小滑块碰撞前与碰撞后的速度；

（3）碰撞后小球的速度；

Answer 1

【答案】（1）H=0.95m （2）3m/s，1m/s（3）v2=2.0m/s

【解析】（1）设小滑块运动到B点的速度为

由机械能守恒定律有：

由牛顿第二定律有：

联立上式解得：

（2）设小滑块运动到C点的速度为，由动能定理有：

可得小滑块在C点的速度即与小球碰前的速度

碰后滑块返回B点过程：由动能定理：

得可碰后滑块速度

（3）碰撞过程由动量守恒：

解得碰后小球速度

综上所述本题答案是：（1），（2）， （3）